Introduction
The regression models in this chapter include the simple and multiple linear regression models, the multivariate general linear model, the polynomial model, and the nonlinear regression model. Functions for fitting regression models, computing summary statistics from a fitted regression, computing diagnostics, and computing confidence intervals for individual cases are provided. Also provided are methods for building a model from a set of candidate variables.
Simple and Multiple Linear Regression
The simple linear regression model is:
yi = β0 + β1 xi + εi i = 1, 2, ..., n
where the observed values of the yi’s constitute the responses or values of the dependent variable, the xi’s are the settings of the independent (explanatory) variable, β0 and β1 are the intercept and slope parameters (respectively), and the εi’s are independently distributed normal errors, each with mean zero and variance σ2. The multiple linear regression model is:
yi = β0 + β1 xi1 + β2 xi2 + ... + βk xik + εi i = 1, 2, ..., n
where the observed values of the yi’s constitute the responses or values of the dependent variable; the xi1’s, xi2’s, ..., xik’s are the settings of the k independent (explanatory) variables; β0, β1, ... , βk are the regression coefficients; and the εi’s are independently distributed normal errors, each with mean zero and variance σ2.
MULTIREGRESS Function fits both the simple and multiple linear regression models using a fast Given’s transformation and includes an option for excluding the intercept β0. The responses are input in array y, and the independent variables are input in array x, where the individual cases correspond to the rows and the variables correspond to the columns. In addition to computing the fit, MULTIREGRESS also can optionally compute summary statistics.
After the model has been fitted using MULTIREGRESS, MULTIPREDICT Function computes predicted values, confidence intervals, and case statistics for the fitted model. The information about the fit is communicated from MULTIREGRESS to MULTIPREDICT by using keyword Predict_Info.
No Intercept Model
Several functions provide the option for excluding the intercept from a model. In most practical applications, the intercept should be included in the model. For functions that use the sum-of-squares and crossproducts matrix as input, the no-intercept case can be handled by using the raw sum-of-squares and crossproducts matrix as input in place of the corrected sum-of-squares and crossproducts. The raw sum-of-squares and crossproducts matrix can be computed as:
(x1, x2, ... , xk, y)T (x1, x2, ... , xk, y)
Variable Selection
Variable selection can be performed by ALLBEST Procedure, which computes all best-subset regressions, or by STEPWISE Procedure, which computes stepwise regression. The method used by ALLBEST is generally preferred over that used by STEPWISE because ALLBEST implicitly examines all possible models in the search for a model that optimizes some criterion while stepwise does not examine all possible models. However, the computer time and memory requirements for ALLBEST can be much greater than that for STEPWISE when the number of candidate variables is large.
Polynomial Model
The polynomial model is:
yi = β0 + β1 xi + β2 x2i + ... + βk xki + εi i = 1, 2, ..., n
where the observed values of the yi’s constitute the responses or values of the dependent variable; the xi’s are the settings of the independent (explanatory) variable; β0, β1, ..., βk are the regression coefficients; and the εi’s are independently distributed normal errors each with mean zero and variance σ2.
Function POLYREGRESS Function fits a polynomial regression model with the option of determining the degree of the model and also produces summary information. Function POLYPREDICT Function computes predicted values, confidence intervals, and case statistics for the model fit by POLYREGRESS.
The information about the fit is communicated from POLYREGRESS to POLYPREDICT by using keyword Predict_Info.
Specification of X for the General Linear Model
Variables used in the general linear model are either continuous or classification variables. Typically, multiple regression models use continuous variables, whereas analysis of variance models use classification variables. Although the notation used to specify analysis of variance models and multiple regression models may look quite different, the models are essentially the same. The term “general linear model” emphasizes that a common notational scheme is used for specifying a model that may contain both continuous and classification variables.
A general linear model is specified by its effects (sources of variation). An effect is referred to in this text as a single variable or a product of variables. (The term “effect” is often used in a narrower sense, referring only to a single regression coefficient.) In particular, an “effect” is composed of one of the following:
Effects of the first type are common in multiple regression models. Effects of the second type appear as main effects in analysis of variance models. Effects of the third type appear as interactions in analysis of variance models. Effects of the fourth type appear in polynomial models and response surface models as powers and crossproducts of some basic variables. Effects of the fifth type appear in analysis of covariance models as regression coefficients that indicate lack of parallelism of a regression function across the groups.
The analysis of a general linear model occurs in two stages. The first stage calls function REGRESSORS Function to specify all regressors except the intercept. The second stage calls MULTIREGRESS Function, at which point the model is specified as either having (default) or not having an intercept.
For the sake of this discussion, define a variable intcep as shown in Table 3-1: intcep Definitions:
Option | intcep | Action |
|---|---|---|
No intercept | 0 | An intercept is not in the model. |
Intercept (default) | 1 | An intercept is in the model. |
The remaining parameters and keywords (n_continuous, n_class, Class_Columns, Var_Effects, and Indices_Effects) are defined for function REGRESSORS. All have defaults except for n_continuous and n_class, both of which must be specified. (See the documentation for the REGRESSORS Function for a discussion of the defaults.) The meaning of each of these input parameters is as follows:
n_continuous—Number of continuous variables.
n_class—Number of classification variables.
Class_Columns—Index vector containing the column numbers of x that are the classification variables.
Var_Effects—Vector containing the number of variables associated with each effect in the model.
Indices_Effects—Index vector containing the column numbers of x for each variable for each effect.
Suppose the data matrix has as its first four columns two continuous variables in Columns 0 and 1 and two classification variables in Columns 2 and 3. The data might appear as shown in Table 3-2: Data Matrix:
Column 0 | Column 1 | Column 2 | Column 3 |
|---|---|---|---|
11.23 | 1.23 | 1.0 | 5.0 |
12.12 | 2.34 | 1.0 | 4.0 |
12.34 | 1.23 | 1.0 | 4.0 |
4.34 | 2.21 | 1.0 | 5.0 |
5.67 | 4.31 | 2.0 | 4.0 |
4.12 | 5.34 | 2.0 | 1.0 |
4.89 | 9.31 | 2.0 | 1.0 |
9.12 | 3.71 | 2.0 | 1.0 |
Each distinct value of a classification variable determines a level. The classification variable in Column 2 has two levels. The classification variable in Column 3 has three levels. (Integer values are recommended, but not required, for values of the classification variables. The values of the classification variables corresponding to the same level must be identical.)
Some examples of regression functions and their specifications are as shown in Table 3-3: Regression Functions:
Regression Functions | intcep | n_class | Class_ Columns | Var_Effects | Indices_ Effects |
|---|---|---|---|---|---|
β0 + β1x1 | 1 | 0 | 1 | 0 | |
β0 + β1x1 + β2x21 | 1 | 0 | 1, 2 | 0, 0, 0 | |
μ + αi | 1 | 1 | 2 | 1 | 2 |
μ + αi + βj + γij | 1 | 2 | 2, 3 | 1, 1, 2 | 2, 3, 2, 3 |
μij | 0 | 2 | 2, 3 | 2 | 2, 3 |
β0 + β1x1 + β2x2 + β3x1x2 | 1 | 0 | 1, 1, 2 | 0, 1, 0, 1 | |
μ + αi + βx1i + βix1i | 1 | 1 | 2 | 1, 1, 2 | 2, 0, 0, 2 |
Functions for Fitting the Model
MULTIREGRESS Function fits a multiple general linear model, where regressors for the general linear model have been generated using REGRESSORS Function.
Linear Dependence and the R Matrix
Linear dependence of the regressors frequently arises in regression models—sometimes by design and sometimes by accident. The functions in this chapter are designed to handle linear dependence of the regressors; i.e., the n × p matrix X (the matrix of regressors) in the general linear model can have rank less than p. Often, the models are referred to as nonfull rank models.
As discussed in Searle (1971, Chapter 5), be careful to correctly use the results of the fitted nonfull rank regression model for estimation and hypothesis testing. In the nonfull rank case, not all linear combinations of the regression coefficients can be estimated. Those linear combinations that can be estimated are called “estimable functions.” If the functions are used to attempt to estimate linear combinations that cannot be estimated, error messages are issued. A good general discussion of estimable functions is given by Searle (1971, pp. 180–188).
The check used by functions in this chapter for linear dependence is sequential. The jth regressor is declared linearly dependent on the preceding j – 1 regressors if 1 – R2j (1, 2, ..., j – 1) is less than or equal to keyword Tolerance. Here, Rj (1, 2, ..., j – 1) is the multiple correlation coefficient of the jth regressor with the first j – 1 regressors. When a function declares the jth regressor to be linearly dependent on the first j – 1, the jth regression coefficient is set to zero. Essentially, this removes the jth regressor from the model.
The reason a sequential check is used is that practitioners frequently include the preferred variables to remain in the model first. Also, the sequential check is based on many of the computations already performed as this does not degrade the overall efficiency of the functions. There is no perfect test for linear dependence when finite precision arithmetic is used. Keyword Tolerance allows the user some control over the check for linear dependence. If a model is full rank, input Tolerance = 0.0. However, Tolerance should be input as approximately 100 times the machine precision. (See function MACHINE.)
Functions performing least squares are based on the QR decomposition of X or on a Cholesky factorization RTR of XTX. Maindonald (1984, Chapters 1–5) discusses these methods extensively. The R matrix used by the regression function is a p × p upper-triangular matrix, i.e., all elements below the diagonal are zero. The signs of the diagonal elements of R are used as indicators of linearly dependent regressors and as indicators of parameter restrictions imposed by fitting a restricted model. The rows of R can be partitioned into three classes by the sign of the corresponding diagonal element:
1. A positive diagonal element means the row corresponds to data.
2. A negative diagonal element means the row corresponds to a linearly independent restriction imposed on the regression parameters by AB = Z in a restricted model.
3. A zero diagonal element means a linear dependence of the regressors was declared. The regression coefficients in the corresponding row of:
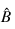
are set to zero. This represents an arbitrary restriction that is imposed to obtain a solution for the regression coefficients. The elements of the corresponding row of R also are set to zero.
Nonlinear Regression Model
The nonlinear regression model is
yi = f(xi ; θ ) + ε i i = 1, 2, ..., n
where the observed values of the yi’s constitute the responses or values of the dependent variable, the xi’s are the known vectors of values of the independent (explanatory) variables, f is a known function of an unknown regression parameter vector θ, and the εi’s are independently distributed normal errors each with mean zero and variance σ2.
NONLINREGRESS Function performs the least-squares fit to the data for this model.
Weighted Least Squares
Functions throughout this chapter generally allow weights to be assigned to the observations. Keyword Weights is used throughout to specify the weighting for each row of X.
Computations that relate to statistical inference—e.g., t tests, F tests, and confidence intervals—are based on the multiple regression model except that the variance of εi is assumed to equal σ2 times the reciprocal of the corresponding weight.
If a single row of the data matrix corresponds to ni observations, keyword Frequencies can be used to specify the frequency for each row of X. Degrees of freedom for error are affected by frequencies but are unaffected by weights.
Summary Statistics
MULTIREGRESS Function can be used to compute statistics related to a regression for each of the q dependent variables fitted. The summary statistics include the model analysis of variance table, sequential sum of squares and F-statistics, coefficient estimates, estimated standard errors, t-statistics, variance inflation factors, and estimated variance-covariance matrix of the estimated regression coefficients POLYREGRESS Function. includes most of the same functionality for polynomial regressions.
The summary statistics are computed under the model y = Xβ + ε, where y is the n × 1 vector of responses, X is the n × p matrix of regressors with rank (X) = r, β is the p × 1 vector of regression coefficients, and ε is the n × 1 vector of errors whose elements are independently normally distributed with mean zero and variance σ2/wi.
Given the results of a weighted least-squares fit of this model (with the wi’s as the weights), most of the computed summary statistics are output in the following keywords:
Anova_Table—One-dimensional array, usually of length 15. In STEPWISE, Anova_Table is of length 13 because the last two elements of the array cannot be computed from the input. The array contains statistics related to the analysis of variance. The sources of variation examined are the regression, error, and total. The first 10 elements of Anova_Table and the notation frequently used for these is described in Table 3-4: Model Analysis of Variance (here, Aov replaces Anova_Table):
Source of Variation | Degrees of Freedom | Sum of Squares | Mean Square | F | p-value |
|---|---|---|---|---|---|
Regression | DFR = Aov (0) | SSR = Aov (3) | MSR = Aov (6) | Aov (8) | Aov (9) |
Error | DFE = Aov (1) | SSE = Aov (4) | s2 = Aov (7) | ||
Total | DFT = Aov (2) | SST = Aov (5) |
If the model has an intercept (default), the total sum of squares is the sum of squares of the deviations of yi from its (weighted) mean:
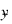
the so-called corrected total sum of squares denoted by the following:
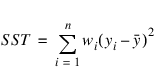
If the model does not have an intercept (No_Intercept), the total sum of squares is the sum of squares of yi—the so-called uncorrected total sum of squares denoted by the following:
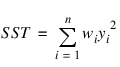
The error sum of squares is given as follows:
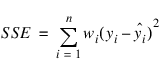
The error degrees of freedom is defined by DFE = n – r.
The estimate of σ2 is given by s2 = SSE/DFE, which is the error mean square.
The computed F statistic for the null hypothesis, H0:β1 = β2 = ... = βk = 0, versus the alternative that at least one coefficient is nonzero is given by F = MSR/s2. The p-value associated with the test is the probability of an F larger than that computed under the assumption of the model and the null hypothesis. A small p-value (less than 0.05) is customarily used to indicate there is sufficient evidence from the data to reject the null hypothesis.
The remaining five elements in Anova_Table frequently are displayed together with the actual analysis of variance table. The quantities R-squared (R2 = Anova_Table(10)) and adjusted R-squared (R2a = Anova_Table(11)) are expressed as a percentage and are defined as follows:
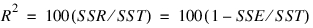
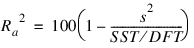
The square root of s2 (s = Anova_Table(12)) is frequently referred to as the estimated standard deviation of the model error.
The overall mean of the responses:
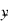
is output in Anova_Table (13).
The coefficient of variation (CV = Anova_Table(14)) is expressed as a percentage and defined by:
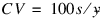
T_Tests—Two-dimensional matrix containing the regression coefficient vector:
as one column and associated statistics (estimated standard error, t statistic and p-value) in the remaining columns.
Coef_Covariances—Estimated variance-covariance matrix of the estimated regression coefficients.
Tests for Lack-of-Fit
Tests for lack-of-fit are computed for the polynomial regression by POLYREGRESS Function. Output keyword Ssq_Lof returns the lack-of-fit F tests for each degree polynomial 1, 2, ..., k, that is fit to the data. These tests are used to indicate the degree of the polynomial required to fit the data well.
Diagnostics for Individual Cases
Diagnostics for individual cases (observations) are computed by two functions in the regression chapter: MULTIPREDICT Function for linear and nonlinear regressions and POLYPREDICT Function for polynomial regressions.
Statistics computed include predicted values, confidence intervals, and diagnostics for detecting outliers and cases that greatly influence the fitted regression.
The diagnostics are computed under the model y = Xβ + ε, where y is the n × 1 vector of responses, X is the n × p matrix of regressors with rank (X) = r, β is the p × 1 vector of regression coefficients, and ε is the n × 1 vector of errors whose elements are independently normally distributed with mean zero and variance σ2/wi.
Given the results of a weighted least-squares fit of this model (with the wi’s as the weights), the following five diagnostics are computed:
1. leverage
2. standardized residual
3. jackknife residual
4. Cook’s distance
5. DFFITS
The definitions of these terms are given in the discussion below.
Let xi be a column vector containing the elements of the ith row of X. A case can be unusual either because of xi or because of the response yi. The leverage hi is a measure of uniqueness of the xi. The leverage is defined by:
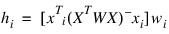
where W = diag(w1, w2, ..., wn) and (XTWX)– denotes a generalized inverse of XTWX. The average value of the hi’s is r/n. Regression functions declare xi unusual if hi > 2r/n. Hoaglin and Welsch (1978) call a data point highly influential (i.e., a leverage point) when this occurs.
Let ei denote the residual:
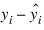
for the ith case.
The estimated variance of ei is (1 – hi)s2/wi, where s2 is the estimated standard deviation of the model error. The ith standardized residual (also called the internally studentized residual) is by definition:
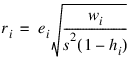
and ri follows an approximate standard normal distribution in large samples.
The ith jackknife residual or deleted residual involves the difference between yi and its predicted value, based on the data set in which the ith case is deleted. This difference equals ei/(1 – hi). The jackknife residual is obtained by standardizing this difference. The residual mean square for the regression in which the ith case is deleted is as follows:
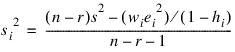
The jackknife residual is defined as:
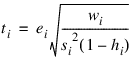
and ti follows a t distribution with n – r – 1 degrees of freedom.
Cook’s distance for the ith case is a measure of how much an individual case affects the estimated regression coefficients. It is given as follows:
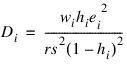
Weisberg (1985) states that if Di exceeds the 50th percentile of the F(r, n – r) distribution, it should be considered large. (This value is about 1. This statistic does not have an F distribution.)
DFFITS, like Cook’s distance, is also a measure of influence. For the ith case, DFFITS is computed by the following formula:
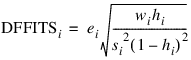
Hoaglin and Welsch (1978) suggest that DFFITS greater than:
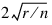
is large.
Transformations
Transformations of the independent variables are sometimes useful in order to satisfy the regression model. The inclusion of squares and crossproducts of the variables (x1, x2, x21, x22, x1x2) often is needed. Logarithms of the independent variables also are used. (See Draper and Smith 1981, pp. 218–222; Box and Tidwell 1962; Atkinson 1985, pp. 177–180; and Cook and Weisberg 1982, pp. 78–86.)
When the responses are described by a nonlinear function of the parameters, a transformation of the model equation often can be selected so that the transformed model is linear in the regression parameters. For example, by taking natural logarithms on both sides of the equation, the exponential model:
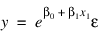
can be transformed to a model that satisfies the linear regression model provided the εi’s have a log-normal distribution (Draper and Smith 1981, pp. 222–225).
When the responses are nonnormal and their distribution is known, a transformation of the responses often can be selected so that the transformed responses closely satisfy the regression model assumptions. The square-root transformation for counts with a Poisson distribution and the arc-sine transformation for binomial proportions are common examples (Snedecor and Cochran 1967, pp. 325–330; Draper and Smith 1981, pp. 237–239).
Alternatives to Least Squares
The method of least squares has desirable characteristics when the errors are normally distributed, e.g., a least-squares solution produces maximum likelihood estimates of the regression parameters. However, when errors are not normally distributed, least squares may yield poor estimators. Function LNORMREGRESS offers three alternatives to least squares methodology, Least Absolute Value, Lp Norm, and Least Maximum Value.
The least absolute value (LAV, L1) criterion yields the maximum likelihood estimate when the errors follow a Laplace distribution. Keyword Lav is often used when the errors have a heavy tailed distribution or when a fit is needed that is resistant to outliers.
A more general approach, minimizing the Lp norm (p ≤ 1), is given by keyword Llp. Although the routine requires about 30 times the CPU time for the case p = 1 than would the use of keyword Lav, the generality of Llp allows the user to try several choices for p ≥ 1 by simply changing the input value of p in the calling program. The CPU time decreases as p gets larger. Generally, choices of p between 1 and 2 are of interest. However, the Lp norm solution for values of p larger than 2 can also be computed.
The minimax (LMV, 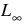 , Chebyshev) criterion is used by setting keyword Lmv. Its estimates are very sensitive to outliers, however, the minimax estimators are quite efficient if the errors are uniformly distributed.
, Chebyshev) criterion is used by setting keyword Lmv. Its estimates are very sensitive to outliers, however, the minimax estimators are quite efficient if the errors are uniformly distributed.
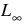 , Chebyshev) criterion is used by setting keyword Lmv. Its estimates are very sensitive to outliers, however, the minimax estimators are quite efficient if the errors are uniformly distributed.
, Chebyshev) criterion is used by setting keyword Lmv. Its estimates are very sensitive to outliers, however, the minimax estimators are quite efficient if the errors are uniformly distributed. Missing Values
NaN (Not a Number) is the missing value code used by the regression functions. Use function MACHINE to retrieve NaN. Any element of the data matrix that is missing must be set to NaN. In fitting regression models, any observation containing NaN for the independent, dependent, weight, or frequency variables is omitted from the computation of the regression parameters.





