ALLBEST Procedure
Selects the best multiple linear regression models.
Usage
ALLBEST, x, y
Input Parameters
x—Two-dimensional array containing the data for the candidate variables.
y—One-dimensional array of length N_ELEMENTS (x(*, 0)) containing the responses for the dependent variable.
Input Keywords
Double—If present and nonzero, double precision is used.
Weights—One-dimensional array of length N_ELEMENTS (x(*, 0)) containing the weight for each row of x. Default: Weights(*) = 1
Frequencies—One-dimensional array of length N_ELEMENTS (x(*, 0)) containing the frequency for each row of x. Default: Frequencies (*) = 1
Max_Subset—The R2 criterion is used, where subset sizes 1, 2, ..., Max_Subset are examined. This option is the default with Max_Subset = N_ELEMENTS (x(0, *)). Keywords Max_Subset, Adj_R_Squared, and Mallows_Cp cannot be used together.
Adj_R_Squared—The adjusted R2 criterion is used, where subset sizes 1, 2, ..., N_ELEMENTS (x(*, 0)) are examined. Keywords Max_Subset, Adj_R_Squared, and Mallows_Cp cannot be used together.
Mallows_Cp—Mallows Cp criterion is used, where subset sizes 1, 2, ..., N_ELEMENTS (x(*, 0)) are examined. Keywords Max_Subset, Adj_R_Squared, and Mallows_Cp cannot be used together.
Max_N_Best—Number of best regressions to be found. If the R2 criterion is selected, the Max_N_Best best regressions for each subset size examined are found. If the adjusted R2 or Mallows Cp criterion is selected, the Max_N_Best overall regressions are found. Default: Max_N_Best = 1
Max_N_Good—Maximum number of good regressions of each subset size to be saved in finding the best regressions. Keyword Max_N_Good must be greater than or equal to Max_N_Best. Normally, Max_N_Good should be less than or equal to 10. It need not ever be larger than the maximum number of subsets for any subset size. Computing time required is inversely related to Max_N_Good. Default: Max_N_Good = 10
Cov_Nobs—Number of observations associated with array Cov_Input. Keywords Cov_Input and Cov_Nobs must be used together.
Cov_Input—Two-dimensional square array of size (N_ELEMENTS (x(0, *)) + 1) by (N_ELEMENTS (x(0, *)) + 1) containing a variance-covariance or sum-of-squares and crossproducts matrix, in which the last column must correspond to the dependent variable.
Array Cov_Input can be computed using function COVARIANCES. Parameters x and y, and keywords Frequencies and Weights are not accessed when this option is specified. Normally, ALLBEST computes Cov_Input from the input data matrices x and y. However, there may be cases when the user wants to calculate the covariance matrix and manipulate it before calling ALLBEST. See the Discussion section for a discussion of such cases.
note | Keywords Cov_Input and Cov_Nobs must be used together. |
Output Keywords
Idx_Criterions—Named variable into which the one-dimensional array of length NSIZE containing the locations in Criterions of the first element for each subset size is stored. NSIZE is calculated as follows: NSIZE = (Max_Subset + 1) if Max_Subset is set. NSIZE = (N_ELEMENTS (x(0, *)) + 1) otherwise. For i = 0, 1, ..., NSIZE – 2, element numbers Idx_Criterions(i), Idx_Criterions (i) + 1, ..., Idx_Criterions(i + 1) – 1 of Criterions correspond to the (i + 1)-st subset size. Keywords Criterions and Idx_Criterions must be used together.
Criterions—Named variable into which the one-dimensional array of length max(Idx_Criterions (NSIZE – 1), N_ELEMENTS (x(0, *)) containing in its first Idx_Criterions (NSIZE – 1) elements the criterion values for each subset considered, in increasing subset size order, is stored. Keywords Criterions and Idx_Criterions must be used together.
Idx_Vars—Named variable into which the one-dimensional array of length NSIZE containing the locations in Indep_Vars of the first element for each subset size. NSIZE is calculated as follows: NSIZE = (Max_Subset + 1) if Max_Subset is set. NSIZE = (N_ELEMENTS(x(0, *)) + 1) otherwise. For i = 0, 1, ..., NSIZE – 2, element numbers Idx_Vars(i), Idx_Vars (i) + 1, ..., Idx_Vars (i + 1) – 1) of Indep_Vars correspond to the (i + 1)-st subset size. Keywords Indep_Vars and Idx_Vars must be used together.
Indep_Vars—Named variable into which the one-dimensional array of length Idx_Vars (NSIZE – 1) containing the variable numbers for each subset considered and in the same order as in Criterions is stored. Keywords Indep_Vars and Idx_Vars must be used together.
Idx_Coefs—Named variable into which the one-dimensional array of length NBEST + 1 containing the locations of Coefficients the first row of each of the best regressions is stored. Here, NTBEST is the total number of best regression found and is Max_Subset * Max_N_Best if Max_Subset is specified, Max_N_Best if either Mallows_Cp or Adj_R_Squared is specified, and Max_N_Best * (N_ELEMENTS (x(0, *))) otherwise. For i = 0, 1, ..., NTBEST, rows Idx_Coefs (i), Idx_Coefs(i) + 1, ..., Idx_Coefs (i + 1) – 1 of Coefs correspond to the (i + 1)-st regression. Keywords Coefs and Idx_Coefs must be used together.
Coefs—Named variable into which the two-dimensional array of size (Idx_Coefs (NTBEST)) × 5 containing statistics relating to the regression coefficients of the best models is stored. Each row corresponds to a coefficient for a particular regression. The regressions are in order of increasing subset size. Within each subset size, the regressions are ordered so that the better regressions appear first. The statistic in the columns are as follows (inferences are conditional on the selected model):
Keywords Coefs and Idx_Coefs must be used together.
Discussion
Procedure ALLBEST finds the best subset regressions for a regression problem with:
n_candidate = (N_ELEMENTS (x (0, *)))
independent variables. Typically, the intercept is forced into all models and is not a candidate variable. In this case, a sum-of-squares and crossproducts matrix for the independent and dependent variables corrected for the mean is computed internally. There may be cases when it is convenient for the user to calculate the matrix; see the description of the Cov_Input optional parameter.
“Best” is defined, on option, by one of the following three criteria:
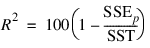
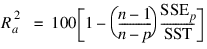
Note that maximizing the criterion is equivalent to minimizing the residual mean square:
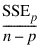
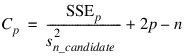
Here, n is equal to the sum of the frequencies (or N_ELEMENTS(x (*, 0)) if Frequencies is not specified) and SST is the total sum of squares. SSEp is the error sum of squares in a model containing p regression parameters including β0 (or p – 1 of the n_candidate candidate variables). Variable is the s2n_candidate error mean square from the model with all n_candidate variables in the model. Hocking (1972) and Draper and Smith (1981, pp. 296–302) discuss these criteria.
Procedure ALLBEST is based on the algorithm of Furnival and Wilson (1974). This algorithm finds Max_N_Good candidate regressions for each possible subset size. These regressions are used to identify a set of best regressions. In large problems, many regressions are not computed. They may be rejected without computation based on results for other subsets; this yields an efficient technique for considering all possible regressions.
There are cases when the user may wish to input the variance-covariance matrix rather than allow the procedure ALLBEST to calculate it. This can be accomplished using keyword Cov_Input. Three situations in which the user may want to do this are as follows:
1. The intercept is not in the model. A raw (uncorrected) sum-of-squares and crossproducts matrix for the independent and dependent variables is required. Keyword Cov_Nobs must be set to 1 greater than the number of observations. Form ATA, where A = [A, Y], to compute the raw sum-of-squares and crossproducts matrix.
2. An intercept is to be a candidate variable. A raw (uncorrected) sum-of-squares and crossproducts matrix for the constant regressor (= 1.0), independent variables, and dependent variables is required for Cov_Input. In this case, Cov_Input contains one additional row and column corresponding to the constant regressor. This row/column contains the sum of squares and crossproducts of the constant regressor with the independent and dependent variables. The remaining elements in Cov_Input are the same as in the previous case. Keyword Cov_Nobs must be set to 1 greater than the number of observations.
3. There are m variables to be forced into the models. A sum-of-squares and crossproducts matrix adjusted for the m variables is required (calculated by regressing the candidate variables on the variables to be forced into the model). Keyword Cov_Nobs must be set to m less than the number of observations.
Programming Notes
Procedure ALLBEST saves considerable CPU time over explicitly computing all possible regressions. However, the procedure has some limitations that can cause unexpected results for users who are unaware of the limitations of the software.
1. For n_candidate + 1 > –log2(ε), where ε is machine precision, some results may be incorrect. This limitation arises because the possible models indicated (the model numbers 1, 2, ..., 2n_candidate ) are stored as floating-point values; for sufficiently large n_candidate, the model numbers cannot be stored exactly. On many computers, this means ALLBEST (for n_candidate > 24; single precision) and ALLBEST (for n_candidate > 49; double precision) can produce incorrect results.
2. Procedure ALLBEST eliminates some subsets of candidate variables by obtaining lower bounds on the error sum of squares from fitting larger models. First, the full model containing all n_candidate is fit sequentially using a forward stepwise procedure in which one variable enters the model at a time, and criterion values and model numbers for all the candidate variables that can enter at each step are stored. If linearly dependent variables are removed from the full model, error STAT_VARIABLES_DELETED is issued. If this error is issued, some submodels that contain variables removed from the full model because of linear dependency can be overlooked if they have not already been identified during the initial forward stepwise procedure. If error STAT_VARIABLES_DELETED is issued and the user wants the variables that were removed from the full model to be considered in smaller models, rerun the program with a set of linearly independent variables.
Example
This example uses a data set from Draper and Smith (1981, pp. 629-630). The ALLBEST procedure is used to find the best regression for each subset size using the Mallow’s Cp statistic as the criterion. Note that when Mallow’s Cp statistic (or adjusted R2) is specified, the variable Max_N_Best indicates the total number of “best” regressions (rather than indicating the number of best regressions per subset size, as in the case of the R2 criterion). In this example, the three best regressions are found to be (1, 2), (1, 2, 4), and (1, 2, 3).
PRO ALLBEST_ex1
; Define the data set.
x = TRANSPOSE( [ [7., 26., 6., 60.], [1., 29., 15., 52.], $
[11., 56., 8., 20.], [11., 31., 8., 47.], $
[7., 52., 6., 33.], [11., 55., 9., 22.], $
[3., 71., 17., 6.], [1., 31., 22., 44.], $
[2., 54., 18., 22.], [21., 47., 4., 26.], $
[1., 40., 23., 34.], $ [11., 66., 9., 12.], $
[10., 68., 8., 12.]])
y = [78.5, 74.3, 104.3, 87.6, 95.9, 109.2, 102.7, 72.5, $
93.1, 115.9, 83.8, 113.3, 109.4]
Max_N_Best = 3
ALLBEST, x, y, Max_N_Best=max_n_best, /Mallows_Cp, $
Idx_Coefs=idx_coefs, Coefs=coefs
; First, the two important matrices, Idx_Coefs and Coefs, are
; printed to display how they appear as output from ALLBEST.
PRINT, ' * * * Idx_Coefs and Coefs in raw form * * *'
PM, idx_coefs, Title='Idx_Coefs:'
PM, Coefs, Title='Coefs'
; Next, describe how to break apart Coefs by regressions
; based on values of Idx_Coefs. Note: NTBEST is defined under
; description of keyword Idx_Coefs.
ntbest = max_n_best
PRINT, ' * * * How Idx_Coefs describes Coefs * * *'
FOR i=0L, ntbest-1 DO $
PRINT, 'regression', i+1, 'begins at row', Idx_Coefs(i),$
' of Coefs.', Format = '(a, i2, a, i2, a)'
PRINT, '* * * Coefs separated by ', 'regressions * * *'
; Next, Coefs is broken apart by regressions, using Idx_Coefs.
; Note: The final element of Idx_Coefs is not a row number but
; instead is equal to the total number of rows in Coefs.
FOR i=0L, ntbest-1 DO BEGIN
start = idx_coefs(i)
stop = idx_coefs(i + 1) - 1
FOR j=start, stop DO BEGIN
PRINT, coefs(j, *), Format='(5f9.4)'
END
END
; Finally, regression labels, column labels, etc., are added.
PRINT, ' * * * Best Regressions* * *'
FOR i=0L, ntbest-1 DO BEGIN
start = idx_coefs(i)
stop = idx_coefs(i + 1) - 1
count = stop - start + 1
PRINT, 'Best Regression with', count, $
'variables(s) (Mallows CP)', Format='(a, i2, a)'
PRINT, $
'variable coefficient std error t p-value'
FOR j=start, stop DO $
PRINT, coefs(j, *), Format='(i5, 2x, 4f11.4)'
END
END
This results in the following output:
* * * Idx_Coefs and Coefs in raw form * * *
PM, Idx_Coefs
0
2
5
8
PM, Coefs
1.00000 1.46831 0.121301 12.1046 2.38419e-07
2.00000 0.662251 0.0458547 14.4424 0.00000
1.00000 1.45194 0.116998 12.4099 5.96046e-07
2.00000 0.416112 0.185611 2.24185 0.0516866
4.00000 -0.236538 0.173288 -1.36500 0.205401
1.00000 1.69589 0.204582 8.28953 1.66893e-05
2.00000 0.656915 0.0442343 14.8508 1.19209e-07
3.00000 0.250018 0.184711 1.35356 0.208889
* * * How Idx_Coefs describes Coefs * * *
regression 1 begins at row 0 of Coefs.
regression 2 begins at row 2 of Coefs.
regression 3 begins at row 5 of Coefs.
* * * Coefs separated by regressions * * *
1.0000 1.4683 0.1213 12.1046 0.0000
2.0000 0.6623 0.0459 14.4424 0.0000
1.0000 1.4519 0.1170 12.4099 0.0000
2.0000 0.4161 0.1856 2.2419 0.0517
4.0000 -0.2365 0.1733 -1.3650 0.2054
1.0000 1.6959 0.2046 8.2895 0.0000
2.0000 0.6569 0.0442 14.8508 0.0000
3.0000 0.2500 0.1847 1.3536 0.2089
* * * Best Regressions* * *
Best Regression with 2 variable(s) (Mallows CP)
variable coefficient std error t p-value
1 1.4683 0.1213 12.1046 0.0000
2 0.6623 0.0459 14.4424 0.0000
Best Regression with 3 variable(s) (Mallows CP)
variable coefficient std error t p-value
1 1.4519 0.1170 12.4099 0.0000
2 0.4161 0.1856 2.2419 0.0517
4 -0.2365 0.1733 -1.3650 0.2054
Best Regression with 3 variable(s) Mallows CP)
variable coefficient std error t p-value
1 1.6959 0.2046 8.2895 0.0000
2 0.6569 0.0442 14.8508 0.0000
3 0.2500 0.1847 1.3536 0.2089
Warning Errors
STAT_VARIABLES_DELETED—At least one variable is deleted from the full model because the variance-covariance matrix Cov is singular.
Fatal Errors
STAT_NO_VARIABLES—No variables can enter any model.





