POLYPREDICT Function
Computes predicted values, confidence intervals, and diagnostics after fitting a polynomial regression model.
Usage
result = POLYPREDICT(predict_info, x)
Input Parameters
predict_info—One-dimensional byte array containing information computed by function POLYREGRESS and returned through keyword Predict_Info. The data contained in this array is in an encrypted format and should not be altered after it is returned by POLYREGRESS.
x—One-dimensional array containing the values of the independent variable for which calculations are to be performed.
Returned Value
result—One-dimensional array containing the predicted values.
Input Keywords
Double—If present and nonzero, double precision is used.
Weights—One-dimensional array containing the weight for each element of x. The computed prediction interval uses SSE/(DFE * Weights (i)) for the estimated variance of a future response. Default: Weights (*) = 1
Confidence—Confidence level for both two-sided interval estimates on the mean and for two-sided prediction intervals, in percent. Keyword Confidence must be in the range (0.0, 100.0). For one-sided intervals with confidence level, where 50.0 ≤ c < 100.0, set Confidence = 100.0 – 2.0 * (100.0 – c). Default: Confidence = 95.0
Y—Array of length N_ELEMENTS (x) containing the observed responses.
Output Keywords
Ci_Scheffe—Named variable into which the two-dimensional array of size 2 by N_ELEMENTS(x) containing the Scheffé confidence intervals, corresponding to the rows of x, is stored. Element Ci_Scheffe (0, i) contains the ith lower confidence limit; Ci_Scheffe(1, i) contains the ith upper confidence limit.
Ci_Ptw_Pop_Mean—Named variable into which the two-dimensional array of size 2 by N_ELEMENTS(x) containing the confidence intervals for two-sided interval estimates of the means, corresponding to the elements of x, is stored. Element Ci_Ptw_Pop_Mean(0, i) contains the ith lower confidence limit, Ci_Ptw_Pop_Mean (1, i) contains the ith upper confidence limit.
Ci_Ptw_New_Samp—Named variable into which the two-dimensional array of size 2 by N_ELEMENTS(x) containing the confidence intervals for two-sided prediction intervals, corresponding to the elements of x, is stored. Element Ci_Ptw_New_Samp(0, i) contains the ith lower confidence limit, Ci_Ptw_New_Samp(1, i) contains the ith upper confidence limit.
Leverage—Named variable into which the one-dimensional array of length N_ELEMENTS(x) containing the leverages is stored.
Residual—Named variable into which the one-dimensional array of length N_ELEMENTS(x) containing the residuals is stored.
Std_Residual—Named variable into which the one-dimensional array of length N_ELEMENTS(x) containing the standardized residuals is stored.
Del_Residual—Named variable into which the one-dimensional array of length N_ELEMENTS(x) containing the deleted residuals is stored.
Cooks_D—Named variable into which the one-dimensional array of length N_ELEMENTS(x) containing the Cook’s D statistics is stored.
Dffits—Named variable into which the one-dimensional array of length N_ELEMENTS(x) containing the DFFITS statistics is stored.
note | You must specify Y when using the Residual, Std_Residual, Del_Residual, Cooks_D, and Dffits keywords. |
Discussion
Function POLYPREDICT assumes a polynomial model:
yi = β 0 + β 1xi + ..., β kxki + εi i = 1, 2, ..., n
where the observed values of the yi’s constitute the response, the xi’s are the settings of the independent variable, the βj’s are the regression coefficients, and the εi’s are the errors that are independently distributed normal with mean zero and the following variance:
σ 2/wi
Given the results of a polynomial regression, fitted using orthogonal polynomials and weights wi, function POLYPREDICT produces predicted values, residuals, confidence intervals, prediction intervals, and diagnostics for outliers and in influential cases.
Often, a predicted value and confidence interval are desired for a setting of the independent variable not used in computing the regression fit. This is accomplished by simply using a different x matrix than was used for the fit when calling POLYPREDICT (POLYREGRESS Function).
Results from function POLYREGRESS, which produces the fit using orthogonal polynomials, are used for input by the array predict_info. The fitted model from POLYREGRESS is:
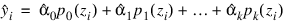
where the zi’s are settings of the independent variable x scaled to the interval [–2, 2] and the pj (z)’s are the orthogonal polynomials. The XTX matrix for this model is a diagonal matrix with elements dj. The case statistics are easily computed from this model and are equal to those from the original polynomial model with βj’s as the regression coefficients.
The leverage is computed as follows:
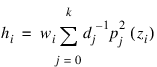
The estimated variance of:
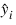
is given by the following:
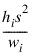
The computation of the remainder of the case statistics follow easily from their definitions. See the chapter introduction for the definition of the case diagnostics.
Often, predicted values and confidence intervals are desired for combinations of settings of the independent variables not used in computing the regression fit. This can be accomplished by defining a new data matrix. Since the information about the model fit is input in predict_info, it is not necessary to send in the data set used for the original calculation of the fit, i.e., only variable combinations for which predictions are desired need be entered in x.
Example 1
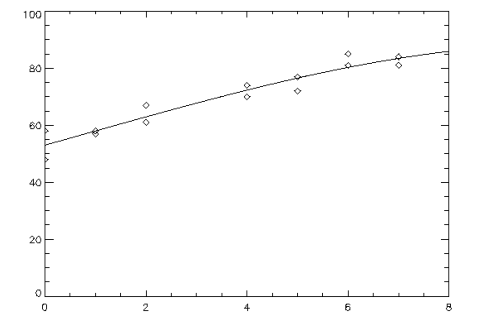
A polynomial model is fit to data using the POLYREGRESS Function), then POLYPREDICT is used to compute predicted values. The results are shown in Figure 3-4: Original and Predicted Values Plot.
; Define the sample data set.
x = [0, 0, 1, 1, 2, 2, 4, 4, 5, 5, 6, 6, 7, 7]
y = [58, 48, 58, 57, 61, 67, 70, 74, 77, 72, 81, 85, 84, 81]
degree = 3
; Call POLYREGRESS using keyword Predict_Info.
Coefs = POLYREGRESS(x, y, degree, Predict_Info = predict_info, $
x2 = 8 * FINDGEN(100)/99)
; Call POLYPREDICT with Predict_Info.
predicted = POLYPREDICT(predict_info, x2)
; Plot the results.
PLOT, x, y, Psym = 4
OPLOT, x2, predicted
 |
Example 2
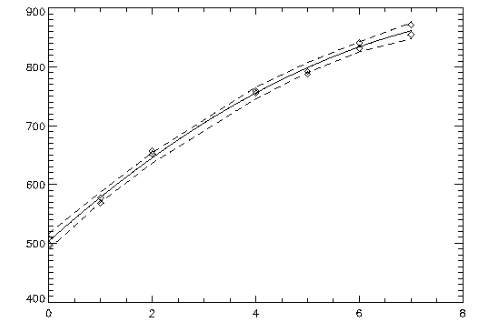
A polynomial model is fit to the data discussed by Neter and Wasserman (1974, pp. 279-285). The data set contains the response variable y measuring coffee sales (in hundreds of gallons) and the number of self-service dispensers. Responses for 14 similar cafeterias are in the data set. First, a procedure is defined to print the ANOVA table. The results are shown in Figure 3-5: Predicted Values with Confidence Bands Plot.
PRO print_results, anova_table
; Define some labels for the anova table.
labels = ['df for among groups ', $
'df for within groups ', $
'total (corrected) df ', $
'ss for among groups ', $
'ss for within groups ', $
'total (corrected) ss ', $
'mean square among groups ', $
'mean square within groups ', $
'F-statistic ', $
'P-value ', $
'R-squared (in percent) ', $
'adjusted R-squared (in percent)', $
'est. std of within group error ', $
'overall mean of y ', $
'coef. of variation (in percent)']
; Print the analysis of variance table.
PRINT, ' * * Analysis of Variance * *'
FOR i=0L, 13 DO PRINT, labels(i), $
anova_table(i), Format = '(a32,f10.2)'
END
x = [0, 0, 1, 1, 2, 2, 4, 4, 5, 5, 6, 6, 7, 7]
y = [508.1, 498.4, 568.2, 577.3, 651.7, 657.0, 755.3, 758.9, $
787.6, 792.1, 841.4, 831.8, 854.7, 871.4]
degree = 2
; Call POLYREGRESS to compute the fit.
coefs = POLYREGRESS(x, y, degree, $
Anova_Table = anova_table, predict_info = predict_info)
; Call POLYPREDICT.
predicted = POLYPREDICT(predict_info, x, $
Ci_Scheffe = ci_scheffe, Y = y, Dffits = dffits)
; Plot the results; confidence bands are dashed lines.
PLOT, x, ci_scheffe(1, *), Yrange = [450, 900], Linestyle = 2
OPLOT, x, ci_scheffe(0, *), Linestyle = 2
OPLOT, x, y, Psym = 4
x2 = 7 * FINDGEN(100)/99
OPLOT, x2, POLYPREDICT(predict_info, x2)
; Print the ANOVA table.
print_results, anova_table
This results in the following output:
* * Analysis of Variance * *
df for among groups 2.00
df for within groups 11.00
total (corrected) df 13.00
ss for among groups 225031.94
ss for within groups 710.55
total (corrected) ss 225742.48
mean square among groups 112515.97
mean square within groups 64.60
F-statistic 1741.86
P-value 0.00
R-squared (in percent) 99.69
adjusted R-squared (in percent) 99.63
est. std of within group error 8.04
overall mean of y 710.99
coef. of variation (in percent) 1.13
 |
Warning Errors
STAT_LEVERAGE_GT_1—Leverage (= #) much greater than 1 is computed. It is set to 1.0.
STAT_DEL_MSE_LT_0—Deleted residual mean square (= #) much less than zero is computed. It is set to zero.
Fatal Errors
STAT_NEG_WEIGHT—Keyword Weights(#) = #. Weights must be nonnegative.





