MULTIPREDICT Function
Computes predicted values, confidence intervals, and diagnostics after fitting a regression model.
Usage
result = MULTIPREDICT(predict_info, x)
Input Parameters
predict_info—One-dimensional byte array containing information computed by MULTIREGRESS and returned through keyword predict_info. The data contained in this array is in an encrypted format and should not be altered after it is returned by MULTIREGRESS.
x—Two-dimensional array containing the combinations of independent variables in each row for which calculations are to be performed.
Returned Value
result—One-dimensional array of length N_ELEMENTS (x(*, 0)) containing the predicted values.
Input Keywords
Double—If present and nonzero, double precision is used.
Weights—One-dimensional array containing the weight for each row of x. The computed prediction interval uses SSE/(DFE * Weights (1)) for the estimated variance of a future response. Default: Weights (*) = 1
Confidence—Confidence level for both two-sided interval estimates on the mean and for two-sided prediction intervals, in percent. Keyword Confidence must be in the range [0.0, 100.0). For one-sided intervals with confidence level, where 50.0 ≤ c < 100.0, set Confidence = 100.0 – 2.0 * (100.0 – c). Default: Confidence = 95.0
Y—Array of length N_ELEMENTS (x(*, 0)) containing observed responses.
Output Keywords
Ci_Scheffe—Named variable into which the two-dimensional array of size 2 by N_ELEMENTS (x(*, 0)) containing the Scheffé confidence intervals corresponding to the rows of x is stored. Element Ci_Scheffe (0, i) contains the ith lower confidence limit; Ci_Scheffe (1, i) contains the ith upper confidence limit.
Ci_Ptw_Pop_Mean—Named variable into which the two-dimensional array of size 2 by N_ELEMENTS (x(*, 0)) containing the confidence intervals for two-sided interval estimates of the means, corresponding to the rows of x, is stored. Element Ci_Ptw_Pop_Mean (0, i) contains the ith lower confidence limit; Ci_Ptw_Pop_Mean (1, i) contains the ith upper confidence limit.
Ci_Ptw_New_Samp—Named variable into which the two-dimensional array of size 2 by N_ELEMENTS (x(*, 0)) containing the confidence intervals for two-sided prediction intervals, corresponding to the rows of x, is stored. Element Ci_Ptw_New_Samp (0, i) contains the ith lower confidence limit; Ci_Ptw_New_Samp (1, i) contains the ith upper confidence limit.
Leverage—Named variable into which the one-dimensional array of length N_ELEMENTS (x(*, 0)) containing the leverages is stored.
Residual—Named variable into which the one-dimensional array of length N_ELEMENTS (x(*, 0)) containing the residuals is stored.
Std_Residual—Named variable into which the one-dimensional array of length N_ELEMENTS (x(*, 0)) containing the standardized residuals is stored.
Del_Residual—Named variable into which the one-dimensional array of length N_ELEMENTS (x(*, 0)) containing the deleted residuals is stored.
Cooks_D—Named variable into which the one-dimensional array of length N_ELEMENTS (x(*, 0)) containing the Cook’s D statistics is stored.
Dffits—Named variable into which the one-dimensional array of length N_ELEMENTS (x(*, 0)) containing the DFFITS statistics is stored.
note | You must specify the Y keyword when using the Residual, Std_Residual, Del_Residual, Cooks_D, and Dffits keywords. |
Discussion
The general linear model used by function MULTIPREDICT is:
y = Xβ + ε
where y is the n × 1 vector of responses, X is the n × p matrix of regressors, β is the p × 1 vector of regression coefficients, and ε is the n × 1 vector of errors whose elements are independently normally distributed with mean zero and the following variance:
σ 2/wi
From a general linear model fit using the wi’s as the weights, function MULTIPREDICT computes confidence intervals and statistics for the individual cases that constitute the data set. Let xi be a column vector containing elements of the ith row of X. Let W = diag(w1, w2, ..., wn). The leverage is defined as hi = (xTi (XTWX)–) xiwi. Put D = diag(d1, d2, ..., dp) with dj = 1 if the jth diagonal element of R is positive and zero otherwise. The leverage is computed as hi = (aTDa)wi , where a is a solution to RTa = xi. The estimated variance of:
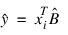
is given by the following:
his2/wi, where s2 = SSE/DFE
The computation of the remainder of the case statistics follow easily from their definitions. See the chapter introduction for definitions of the case diagnostics.
Informational errors can occur if the input matrix X is not consistent with the information from the fit (contained in predict_info), or if excess rounding has occurred. The warning error STAT_NONESTIMABLE arises when X contains a row not in the space spanned by the rows of R. An examination of the model that was fitted and the X for which diagnostics are to be computed is required in order to ensure that only linear combinations of the regression coefficients that can be estimated from the fitted model are specified in x. For further details, see the discussion of estimable functions given in Maindonald (1984, pp. 166–168) and Searle (1971, pp. 180–188).
Often predicted values and confidence intervals are desired for combinations of settings of the independent variables not used in computing the regression fit. This can be accomplished by defining a new data matrix. Since the information about the model fit is input in predict_info, it is not necessary to send in the data set used for the original calculation of the fit, i.e., only variable combinations for which predictions are desired need be entered in x.
Example 1
This example calls MULTIPREDICT to compute predicted values after calling MULTIREGRESS.
; Define the data set.
x = MAKE_ARRAY(13, 4)
x(0, *) = [7, 26, 6, 60]
x(1, *) = [1, 29, 15, 52]
x(2, *) = [11, 56, 8, 20]
x(3, *) = [11, 31, 8, 47]
x(4, *) = [7, 52, 6, 33]
x(5, *) = [11, 55, 9, 22]
x(6, *) = [3, 71, 17, 6]
x(7, *) = [1, 31, 22, 44]
x(8, *) = [2, 54, 18, 22]
x(9, *) = [21, 47, 4, 26]
x(10, *) = [1, 40, 23, 34]
x(11, *) = [11, 66, 9, 12]
x(12, *) = [10, 68, 8, 12]
y = [78.5, 74.3, 104.3, 87.6, 95.9, 109.2, $
102.7, 72.5, 93.1, 115.9, 83.8, 113.3, 109.4]
; Call MULTIREGRESS to compute the fit.
coefs = MULTIREGRESS(x, y, Predict_Info = predict_info)
; Call MULTIPREDICT to compute predicted values.
predicted = MULTIPREDICT(predict_info, x)
; Output the predicted values.
PM, predicted, Title = 'Predicted values'
This results in the following output:
Predicted values
78.4952
72.7888
105.971
89.3271
95.6492
105.275
104.149
75.6750
91.7216
115.618
81.8090
112.327
111.694
Example 2
This example uses the same data set as the first example and also uses a number of keywords to retrieve additional information from MULTIPREDICT. First, a procedure is defined to print the results.
PRO print_results, anova_table, t_tests, y, $
predicted, ci_scheffe, residual, dffits
labels = ['df for among groups ', $
'df for within groups ', $
'total (corrected) df ', $
'ss for among groups ', $
'ss for within groups ', $
'total (corrected) ss ', $
'mean square among groups ', $
'mean square within groups ', $
'F-statistic ', $
'P-value ', $
'R-squared (in percent) ', $
'adjusted R-squared (in percent)', $
'est. std of within group error ', $
'overall mean of y ', $
'coef. of variation (in percent) ']
; Print the analysis of variance table.
PRINT, ' * * Analysis of Variance * *'
PM, [[labels], [STRING(anova_table, Format = '(f11.4)')]]
PRINT, 'Coefficient s.e. t p-value'
PM, t_tests, Format = '(f7.2, 4x, 3f7.2)'
PRINT, ' observed predicted lower upper residual dffits'
PM, [[y], [predicted], [transpose(ci_scheffe)], $
[residual], [dffits]], Format = '(6f10.2)'
END
x = MAKE_ARRAY(13, 4)
x(0, *) = [7, 26, 6, 60]
x(1, *) = [1, 29, 15, 52]
x(2, *) = [11, 56, 8, 20]
x(3, *) = [11, 31, 8, 47]
x(4, *) = [7, 52, 6, 33]
x(5, *) = [11, 55, 9, 22]
x(6, *) = [3, 71, 17, 6]
x(7, *) = [1, 31, 22, 44]
x(8, *) = [2, 54, 18, 22]
x(9, *) = [21, 47, 4, 26]
x(10, *) = [1, 40, 23, 34]
x(11, *) = [11, 66, 9, 12]
x(12, *) = [10, 68, 8, 12]
y = [78.5, 74.3, 104.3, 87.6, 95.9, 109.2, $
102.7, 72.5, 93.1, 115.9, 83.8,113.3, 109.4]
coefs = MULTIREGRESS(x, y, $
Anova_Table = anova_table, $
T_Tests = t_tests, $
Predict_Info = predict_info, $
Residual = residual)
; Call MULTIREGRESS to compute the fit.
predicted = MULTIPREDICT(predict_info, x, $
Ci_scheffe = ci_scheffe, $
Y = y, $
Dffits = dffits)
print_results, anova_table, t_tests, y, $
predicted, ci_scheffe, residual, dffits
This results in the following output:
* * Analysis of Variance * *
df for among groups 4.0000
df for within groups 8.0000
total (corrected) df 12.0000
ss for among groups 2667.8997
ss for within groups 47.8637
total (corrected) ss 2715.7634
mean square among groups 666.9749
mean square within groups 5.9830
F-statistic 111.4791
P-value 0.0000
R-squared (in percent) 98.2376
adjusted R-squared (in percent) 97.3563
est. std of within group error 2.4460
overall mean of y 95.4231
coef. of variation (in percent) 2.5633
Coefficient s.e. t p-value
62.41 70.07 0.89 0.40
1.55 0.74 2.08 0.07
0.51 0.72 0.70 0.50
0.10 0.75 0.14 0.90
-0.14 0.71 -0.20 0.84
observed predicted lower upper residual dffits
78.50 78.50 70.70 86.29 0.00 0.00
74.30 72.79 66.73 78.85 1.51 0.52
104.30 105.97 97.99 113.95 -1.67 -1.24
87.60 89.33 83.62 95.03 -1.73 -0.53
95.90 95.65 89.37 101.93 0.25 0.09
109.20 105.27 101.57 108.98 3.93 0.76
102.70 104.15 97.79 110.51 -1.45 -0.55
72.50 75.67 68.96 82.39 -3.17 -1.64
93.10 91.72 86.02 97.42 1.38 0.42
115.90 115.62 106.83 124.41 0.28 0.30
83.80 81.81 74.96 88.66 1.99 0.93
113.30 112.33 106.94 117.71 0.97 0.26
109.40 111.69 105.91 117.48 -2.29 -0.76
Warning Errors
STAT_NONESTIMABLE—Within the preset tolerance, the linear combination of regression coefficients is nonestimable.
STAT_LEVERAGE_GT_1—Leverage (= #) much greater than 1.0 is computed. It is set to 1.0.
STAT_DEL_MSE_LT_0—Deleted residual mean square (= #) much less than zero is computed. It is set to zero.
Fatal Errors
STAT_NONNEG_WEIGHT_REQUEST_2—Weight for row # was #. Weights must be nonnegative.





