3.3 Logistic Regression

Logistic regression is used to model the relationship between a binary response variable and one or more predictor variables, which may be either discrete or continuous. Binary outcome data is common in medical applications. For example, the binary response variable might be whether or not a patient is alive five years after treatment for cancer or whether the patient has an adverse reaction to a new drug. As in multiple regression, we are interested in finding an appropriate combination of predictor variables to help explain the binary outcome.

Let be a dichotomous random variable denoting the outcome of some experiment, and let be a collection of predictor variables. Denote the conditional probability that the outcome is present by , where has the form:

.

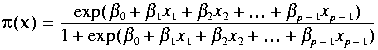If the are varied and the values of are observed, we write:

.

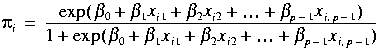The logistic regression problem is then to obtain an estimate of the vector:

.

As with multiple linear regression, the matrix:

,

is called the regression matrix, while the matrix R, containing only the data for the predictor variables (matrix X without the leading column of 1s), is called the predictor data matrix.

The method used to find the parameter estimates is the method of maximum likelihood. Specifically, is the value that maximizes the likelihood function:

.

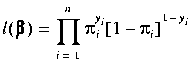The log of this equation is called the log likelihood, and is defined as:

.

Estimates for the variances and covariances of the estimated parameters are computed using the following equations.

Let , where is the matrix regression matrix, and is an diagonal matrix with i^th diagonal term . That is, the matrix is:

and the matrix is:

.

Denote:

.

The estimate of the variance of is then the j^th diagonal term of the matrix , and the off-diagonal terms are the covariance estimates for and .

In practice, several different measures exist for determining the significance, or goodness of fit, of a logistic regression model. These measures include the G statistic, Pearson statistic, and Hosmer-Lemeshow statistic. In a theoretical sense, all three measures are equivalent. To be more precise, as the number of rows in the predictor matrix goes to infinity, all three measures converge to the same estimate of model significance. However, for any practical regression problem with a finite number of rows in the predictor matrix, each measure produces a different estimate.

Commonly a regression model designer refers to more than one measure. If any single measure indicates a low goodness of fit, or if the measures differ greatly in their assessments of significance, the designer goes back and makes improvements to the regression model.

Perhaps the most straightforward measure of a goodness of fit is the G statistic.¹ It is a close analogue to the F statistic for linear regression. Both the F statistic and the G statistic measure a difference in deviance between two models. For logistic regression, the deviance of a model is defined as:

.

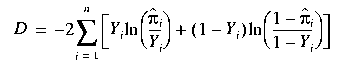To determine the overall significance for a model using the G statistic, the deviance for the model and the deviance for the intercept-only model are subtracted. The larger the difference, the greater the evidence that the model is significant. The G statistic follows a chi-squared distribution with p - 1 degrees of freedom, where p is the number of parameters in the model. Significance tests based on this distribution are supported in Analytics.h++.

The Pearson statistic is a model significance measure based more directly on residual prediction errors. In the most straightforward implementation of the Pearson statistic, the predictor matrix rows are placed into J groups such that identical rows are placed in the same group. Then the Pearson statistic is obtained by summing over all J groups:

,

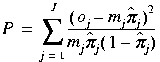where is the number of positive observations for group j, is the model's predicted value, and is the number of identical rows. The Pearson statistic follows a chi-squared distribution with degrees of freedom, where p is the number of parameters in the model. Significance tests based on this distribution are supported in Analytics.h++.

Because the accuracy of this statistic is poor when predictor variable data are continuous-valued,² the statistic in our implementation is obtained by grouping the predictor variable data. In other words, the data values for each predictor variable are replaced with integer values, the logistic regression parameters are recalculated, and the statistic is obtained from the resulting model. This tends to make the value of J much smaller, and the Pearson statistic becomes more accurate. In Analytics.h++, the default number of groups for each predictor variable is 2.

The Hosmer-Lemeshow statistic takes an alternative approach to grouping: it groups the predictions of a logistic regression model rather than the model's predictor variable data, which is the Pearson statistic's approach. In the implementation found in Analytics.h++, model predictions are split into G bins that are filled as evenly as possible.³ Then the statistic is computed as:

,

where is the number of positive observations in group j, is the model's average predicted value in group j, and is the size of the group. The Hosmer-Lemeshow statistic follows a chi-squared distribution with G - 2 degrees of freedom. In Analytics.h++, the default value for G is 10.

For each estimated parameter , the Wald chi-square statistic is the quantity:

,

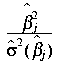where is the estimated variance of as defined in Section 3.3.2.

The p-value for each parameter estimate is the probability of seeing the value of the calculated parameter using the above formula, or something more extreme, if the hypothesis is true. Note that in general the sample size must be large in order for the p-value to be accurate.

The critical values, , for the parameter estimates are the levels at which, if the absolute value of the Wald chi-square statistic calculated for a given is greater than , we reject the hypothesis at the specified significance level.

©Copyright 1999, Rogue Wave Software, Inc.
Contact Rogue Wave about documentation or support issues.