In the late 1880s, Francis Galton was studying the inheritance of physical characteristics. In particular, he wondered if he could predict a boy's adult height based on the height of his father. Galton hypothesized that the taller the father, the taller the son would be. He plotted the heights of fathers and the heights of their sons for a number of father-son pairs, then tried to fit a straight line through the data. If we denote the son's height by
and the father's height by
, we can say that in mathematical terms, Galton wanted to determine constants
and
such that:
.
This is an example of a simple linear regression problem with a single predictor variable,
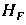. The parameter
is called the intercept parameter. In general, a regression problem may consist of several predictor variables. Thus the multiple linear regression problem may be stated as follows:
Let
be a random variable that can be expressed in the form:
,
where
are known constants, and
is a fluctuation error. The problem is to estimate the parameters
. If the
are varied and the
values
of
are observed, then we write:
,
where
is the ith value of
. Writing these n equations in matrix form we have:
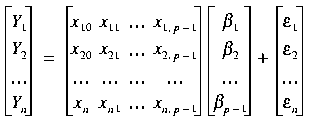
or:
,
where
.
We call the
matrix
the regression matrix,
the response variable,
the response vector, and
the predictor variable.
The method of least squares consists of minimizing
with respect to
. Setting
, we minimize:
subject to:
.
Let
be the least squares estimate of
. The fitted regression
is denoted by:
.
The elements of
are called the residuals. The value of:
is called the residual sum of squares. The matrix:
,
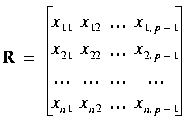which is the regression matrix without the first column of 1s, is called the predictor data matrix.
The variance of the model is defined to be the variance of
. The statistic:
is an unbiased estimator of this variance.
The dispersion matrix for the parameter estimates
is the matrix
, where
is the covariance of
and
. The dispersion matrix is calculated according to the formula:
,
where
is the estimated variance, as defined above, and
and
are the regression matrix and its transpose, respectively.
The overall F statistic is a statistic for testing the null hypothesis
. It is defined by the equation:
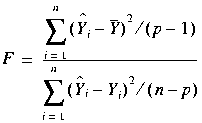, where
.
This statistic follows an F distribution with (p-1) and (n-p) degrees of freedom.
The p-value is the probability of seeing the value of the F statistic for a given linear regression if the null hypothesis:
is true.
The critical value of the F statistic for a specified significance level,
, is the value,
, of the F statistic such that if the F statistic calculated for the multiple linear regression is greater than
, we reject the hypothesis
at the significance level
.
Let
be the estimate for element j of the parameter vector
. The T statistic for the parameter estimate
is a statistic for testing the hypothesis that
. It is calculated according to the formula:
,
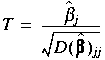where
is the jth diagonal element of the dispersion matrix. This statistic is assumed to follow a T distribution with
degrees of freedom.
The p-value for each parameter estimate
is the probability of seeing the value of the calculated parameter using the formula in Section 3.2.5 if the hypothesis
is true.
The critical value of a parameter T statistic for a given level of significance
is the value
, such that if the absolute value of the T statistic calculated for a given parameter
is greater than
, we reject the hypothesis
at the significance level
.
Suppose that we have calculated parameter estimates
for our linear regression problem. Suppose further that we have a vector of values,
, for the predictor variables. We may obtain an
level confidence interval for the value
, which is the value of the dependent of the observed variable predicted by our model, according to the formula:
,
where
is the value at
of the cumulative distribution function for a T distribution,
is the estimated variance, and
is the regression matrix.
©Copyright 1999, Rogue Wave Software, Inc.
Contact Rogue Wave about documentation or support issues.