Nonsymmetric Eigenvalue Problems
Defining the Problem
The basic nonsymmetric eigenvalue problem is the same as the symmetric. The problem is to find the eigenvalues, l, and the right eigenvectors, p, which satisfy:
Ap = 1p
for a matrix A. This problem is a little more complicated, however, because the eigenvalues are no longer necessarily real; they may be complex, even for real-valued matrices. We may also be interested in the closely-related problem of finding the left eigenvectors, q, which satisfy: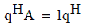
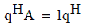
where H is the conjugate transpose of a vector or matrix.
In the last chapter, we presented the Linear Algebra Module object types for solving symmetric eigenvalue problems. This chapter presents the types used in nonsymmetric eigenvalue problems. In addition to the eigenvalue decomposition and server objects, there are objects for representing Schur, Hessenberg, and balance decompositions.





