Understanding the behavior of model selection tools is easiest when the model selection techniques are viewed as search techniques. The search space consists of possible subsets of predictor variables. An evaluation criterion assigns each subset a numerical value, and the goal of the search is to find the subset with the highest numerical value. The only difference between techniques involves the choice of a starting subset and the specification of neighboring subsets in the search space.

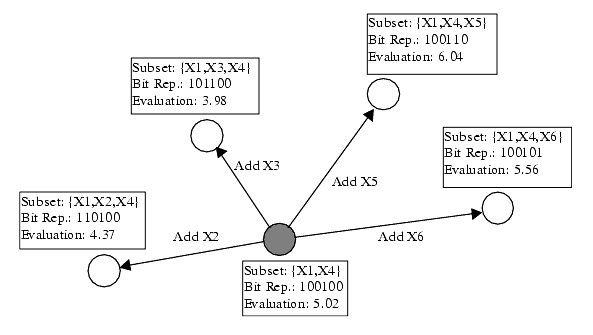
As an example, Figure 3 illustrates one model selection technique, forward selection, using a connected graph. In this particular example, there are six possible predictor variables: { X1, ... , X6 }. Nodes in the graph indicate predictor variable subsets; each node is labeled with the subset, a bit representation of the subset, and the subset’s evaluation criterion. The current node in the search is shaded, while its neighboring nodes are not shaded. Graph edges indicate which subsets are considered neighbors in the search; edges are labeled with the action that changes the current subset into its neighbor. Search continues along the path in the graph that leads to the greatest evaluation criterion, and stops when the evaluation criterion can no longer improve. In the graph in Figure 3, forward selection adds the predictor variable X5 because the resulting predictor variable subset has the highest evaluation criterion with a value of 6.04. Then forward selection makes this subset the current one and continues by evaluating the new subset’s neighbors. The new neighbors are not shown in the figure.