SOBEL Function
Performs a Sobel edge enhancement of an image.
Usage
result = SOBEL(image)
Input Parameters
image—The two-dimensional array containing the image to be enhanced.
Returned Value
result—A two-dimensional array of integer type containing the image that has been edge-enhanced. It has the same dimensions as image.
Keywords
Col—Computes the column gradient (horizontal line enhancement). (Default: Col = 1)
note | For horizontal line enhancement only, set the keyword Row = 0 to disable the vertical line enhancement. |
Edge—A scalar string indicating how edge effects are handled. (Default: 'zero') Valid strings are:
'zero'—Sets the border of the output image to zero. (Default)
'copy'—Copies the border of the input image to the output image.
No_Clip—If set, the result data type is greater than the image data type so that overflow values in result are not clipped.
note | Use the No_Clip keyword to avoid overflow conditions. |
Return—A scalar string specifying a mathematical function to apply. Valid strings are 'abs', 'phase', and 'value'. The Return keyword is used with the Row and Col keywords per Table 16-3: Return Values. (Default: 'abs')
Return = 'abs' | Return = 'phase' | Return = 'value' | |
|---|---|---|---|
Col = 1, Row = 0 | ABS(col grad) | Invalid Condition | column gradient |
Col = 0, Row = 1 | ABS(row grad) | Invalid Condition | row gradient |
Col = 1, Row = 1 | ABS(row grad)+ ABS(col grad) | ATAN(row grad ÷ col grad), data type is double | Invalid Condition |
Col = 0, Row = 0 | Invalid Condition | Invalid Condition | Invalid Condition |
Row—Computes the row gradient (vertical line enhancement). (Default: Row = 1)
note | For vertical line enhancement only, you must disable the horizontal line enhancement by setting the Col keyword to 0. |
Same_Type—If set, the result is the same data type as image; otherwise, the result image data type is always integer unless No_Clip is set.
Scale—If set, each gradient is scaled by the factor 0.25; otherwise, no scaling is performed.
Zero_Negatives—If set, all negative values in the result are set to zero.
Discussion
The SOBEL function supports multi-layer band interleaved images. When the input array is three-dimensional, it is automatically treated as an array of images, array(m, n, p), where p is the number of m-by-n images. Each image is then operated on separately and an array of the result images is returned.
SOBEL implements an approximation of the 3-by-3 nonlinear edge enhancement operator:
G(j,k) = |X| + |Y|
where:
X = (A2 + 2A3 + A4) – (A0 + 2A7 + A6)
Y = (A0 + 2A1 + A2) – (A6 + 2A5 + A4)
and where the pixels surrounding the neighborhood of the pixel F(j, k) are numbered as follows:
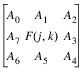
This algorithm is a fast approximation of the SOBEL function, which is actually defined as:
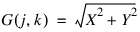
note | Because the result image is saved in integer format, large original data values will cause overflow. Overflow occurs when the absolute value of the result is larger than 32,767. Use the No_Clip keyword to avoid overflow. |
Sample Usage
SOBEL is commonly used to obtain an image that contains only the edges (rapid transitions between light and dark, or from one color to another) that were present in the original image. SOBEL can help enhance features and transitions between areas in an image (for example, a machine part photographed against a white background).
With this information, it is possible to identify and compare features or items in an image with those in another image, usually for verification or detection purposes. SOBEL and other edge-detection algorithms are used extensively for image processing and preprocessing for pattern recognition.
The image returned by SOBEL contains the edges present in the original image, with the brightest edges representing a rapid transition (well-defined features), and darker edges representing smoother transitions (blurred or blended features).
An original image can also be somewhat sharpened by adding or averaging the edge-detected image with the original image.
Example
Figure 16-11: Image Enhanced with the SOBEL Function shows what an aerial image looks like before and after applying the SOBEL function.
 |
See Also





