CONVOL Function
Performs convolution or weighted smoothing.
Usage
result = CONVOL(array, kernel[, scale_factor])
Input Parameters
array—The array to be convolved. The array can be of any data type except string.
kernel—The array used to convolve each value in array. The dimensions of kernel must be smaller than those of array, but they can be of any data type except string. (If a string array is used, PV-WAVE attempts to convert it and then issue an error message.)
scale_factor—(optional) A scaling factor that reduces each output value by the specified factor. The scale_factor parameter can be used with integer and byte type data only. (Default: 1.0)
Returned Value
result—The convolved array of the same data type and dimensions as array.
Keywords
Center—Specifies how to center the kernel. If nonzero or not specified, centers the kernel over each array data point. If explicitly set to zero, centers the kernel a half-kernel width to the left of each array data point. When Center is nonzero, the operation amounts to weighted smoothing.
Edge—A scalar string indicating how edge effects are handled. (Default: 'zero') Valid strings are:
'zero'—Sets the border of the output image to zero. (Default)'copy'—Copies the border of the input image to the output image.Zero_Negatives—If set, all negative values in the result are set to zero.
Discussion
Convolution is a general process that can be used in smoothing, signal processing, shifting, edge detection, and other filtering functions. Therefore, it is often used in conjunction with other functions, such as DIGITAL_FILTER, SMOOTH, and SHIFT.
note | When using CONVOL with image data, make sure the data has been first converted to floating-point type. |
The kernel parameter is an array whose dimensions describe the size of the neighborhood surrounding the value in array that is analyzed. The kernel also includes values that give a weighting to each point in its array. These weightings determine the average that is the value in the output array. If kernel is not of the same type as array, a copy is made and converted into the same type before being used.
Using the scale_factor parameter allows you to simulate fractional kernel values and avoid overflow with byte parameters.
In many signal and image processing applications, it is useful to center a symmetric kernel over the data, to align the result with the original array. The Center keyword controls the alignment of the kernel with the array and the ordering of the kernel elements.
Sample Usage
In the convolution of any two functions, r(t) and s(t), for most applications function s is typically a signal or data stream, which goes on indefinitely in time, while r is a response function, typically a peaked function that falls to zero in both directions from its maximum.
In terms of CONVOL parameters, s corresponds to array and r corresponds to kernel. The effect of convolution is to smear the signal s(t) in time according to the “recipe” provided by the response function r(t).
One-Dimensional Convolution
For the example below, assume the following equation:
R = CONVOL(A, K, S)
where A is an n-element vector, K is an m-element vector (m < n), and S is the scale factor.
If the Center keyword is set to 0, the results are as follows:When t ≥ m – 1, then:
Otherwise, Rt = 0.If the Center keyword is omitted or set to 1, the results are shown as follows.When (m – 1)/2 ≤ t ≤ n – 1 – (m – 1)/2, then:
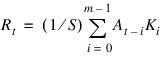
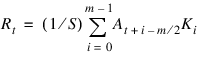
Otherwise, Rt = 0.Two-Dimensional Convolution
For the second example, assume the same equation:
R = CONVOL(A, K, S)
where A is an m-by-n element array, K is an l-by-l element kernel, S is the scale factor, and the result R is an m-by-n element array.
If the Center keyword is set to 0, the results are as follows.When t ≥ l – 1 and u ≥ l – 1, then:
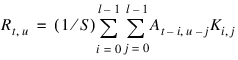
Otherwise, Rt,u = 0.The centered two-dimensional case is similar, except the t –i and u – j subscripts are replaced by t + i – l/2 and u + j – l/2.Example
This example demonstrates what a 512-by-512 mandrill image looks like before and after applying the CONVOL function. The following parameters were used:
; Open and read the mandril image file
OPENR, lun, !Data_dir + 'mandril.img', /Get_lun
mandril_img = BYTARR(512, 512)
READU, lun, mandril_img
FREE_LUN, lun
WINDOW, 2, Xsize=512, Ysize=512, Title='Original Image'
TV, mandril_img
; Define a 3-by-3 array used to convolve the input array.
; The values represent a commonly used algorithm for edge enhancement.
kernel = INTARR(3, 3) + 1
kernel(*,0) = -1
kernel(1,1) = -2
PM, kernel, Title='Kernel values:'
result = CONVOL(mandril_img, kernel, /Center)
WINDOW, 0, Xsize=512, Ysize=512, Title='Image with Enhanced Edges'
TV, result
where kernel is a 3-by-3 array. This array has the following value:
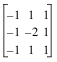
This kernel value represents a commonly-used algorithm for edge enhancement.
Figure 4-8: Using CONVOL to Enhance Edges shows the results of this example. The CONVOL function has been used to enhance the edges of this 512-by-512 mandrill image. In other words, after CONVOL is applied, the dark colors change quickly to light ones.
 |
See Also
For more information on displaying images, see the PV‑WAVE User’s Guide.
For a signal processing example, see the DIGITAL_FILTER Example section.
