FFT Function
Returns the fast Fourier transform (FFT) for the input variable.
Usage
result = FFT(array, direction)
Input Parameters
array—The array for which the FFT or the reverse FFT is computed. The size of each dimension may be any positive integer value.
note | For best results the input arrays should be of type DOUBLE and not FLOAT. |
direction—A signed scalar value that determines the direction of the transform, between the time (or spatial) domain and the frequency domain.
Returned Value
result—The fast Fourier transform of array. The Cooley-Tukey fast Fourier transform algorithm is used for calculating the FFT.
Keywords
Intleave—A scalar string indicating the type of interleaving of 2D input signals containing signal-interleaved signals; and 3D input arrays containing image-interleaved images, or a volume. Valid strings and the corresponding interleaving methods are:
Discussion
The FFT function supports input arrays composed of multiple images (multi-layer band interleaved images) as well as input arrays composed of multiple signals. The Intleave keyword is used to specify whether the input array is a multi-signal or multi-image array. When the Intleave keyword is used to indicate multiple signals or images in this way, each signal or image in the array is operated on separately and an array of the individual results is returned.
The Fourier transform of a scaled-time function is defined by:
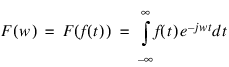
where w relates to the frequency domain, and t relates to the time (space) domain.
The data type of array is converted to complex, with the real part described by array and the imaginary part set to 0, unless it is already complex. The output array will have the same number and size of dimensions as array.
note | For more efficient transforms, choose dimensions for array that are a power of 2. |
The direction parameter controls the direction of the transform:
A normalization factor of 1/n, where n is the number of points in array, is applied to the transformation when going from space to frequency.
note | Take care to avoid wrap-around artifacts when filtering and convolving in the frequency domain. In particular, make sure your images are properly windowed and sampled before applying the Fast Fourier Transform, or false and misleading values will result. |
Example 1
This example shows what an aerial image looks like before and after applying the FFT function, in conjunction with other functions.
The FFT function is used to transform the image into the frequency domain. For the example shown in Figure 7-1: Using the FFT Function PV‑WAVE makes it easy to generate the Fourier spectrum for any image. Note that the diagonal, vertical, and horizontal lines in the Fourier spectrum correspond to the roads in the original 512-by-512 image, but are perpendicular to them; this is because of the 90-degree phase shift that occurs when moving from the space domain to the frequency domain., the following parameters are used:
OPENR, lun, !Dir + '/demo/gallery3/data/aerial_demo.img', /Get_lun
aerial_img = BYTARR(512,512)
READU, lun, aerial_img
FREE_LUN, lun
WINDOW, Xsize=512, Ysize=512
TVSCL, aerial_img
fft_aerial = FFT(aerial_img, -1)
FFT places the frequency component into the first element of the image, which appears in the lower-left corner. However, it is customary to display Fourier spectra of images with the frequency component in the center of the image. This can be done using the SHIFT function to move the origin to the center, and the ABS and ALOG functions to convert the data back into a format that can be displayed:
 |
The result of the initial FFT operation (fft_aerial) can be run through these other three functions as follows:
display = SHIFT(ALOG(ABS(fft_aerial)), 256, 256)
TVSCL, display
The resulting variable, display, is the image displayed on the right in Figure 7-1: Using the FFT Function.
Example 2
For an example of an FFT used in windowing, see the description of the HANNING function.
See Also
For background information, see the PV‑WAVE User’s Guide.
For details on the Cooley-Tukey Fast Fourier Transform algorithm, see the Special Issue on FFT in IEEE Audio Transactions, June 1967.





