HANNING Function
Standard Library function that implements a window function for Fast Fourier Transform signal or image filtering.
Usage
result = HANNING(col[, row])
Input Parameters
col—The number of columns in the result.
row—(optional) The number of rows in the result.
Returned Value
result—The processed result.
Keywords
None.
Discussion
HANNING is a window function for signal or image filtering using a fast fourier transform. By processing data through HANNING before applying FFT, more realistic results can be obtained.
The window calculated by HANNING is basically the first half of a cosine—in other words, only the positive cosine values. When used with only the col parameter, HANNING returns a vector of the same length as col. The vector starts and ends with zeros and rises to a peak in the center (just as a cosine goes up and then comes back down to zero).
For one dimension, the result of HANNING is determined by the following equation:
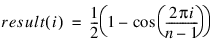
where n is the total number of elements described by row and col.
When used with both the col and row parameters, HANNING returns an array whose dimensions are the same as these two parameters. The resultant array has zeros around the sides and rises to a peak in the center.
For two dimensions, the result (i, j) = result(i) * result(j).
Example
; Open the mandrill image file.
OPENR, unit, !Data_dir + 'mandril.img', /Get_lun
; Store the image.
aa = ASSOC(unit, BYTARR(512, 512))
image = aa(0)
; Close the logical unit number.
FREE_LUN, unit
; Create the HANNING window.
han = HANNING(512, 512)
; Create an FFT of the image without the HANNING window.
a = FFT(image, -1)
WINDOW, 0, XSize=512, YSize=512, $
Title='FFT without HANNING Window Applied'
; Shifting makes it easier to see.
TVSCL, SHIFT(ALOG(ABS(a)), 256, 256)
; Create an FFT of the image with the HANNING window.
; This diminishes the effect of the outside edges of
; the image on the FFT result.
b = FFT(image * han, -1)
WINDOW, 2, Xsize=512, Ysize=512, $
Title='FFT with HANNING Window Applied'
; Look at the result for comparison, and notice that
; the vertical and horizontal streaking is gone.
TVSCL, SHIFT(ALOG(ABS(b)), 256, 256)
See Also
For details on how processing data through HANNING before applying FFT improves results, see Chapter 5 in Digital Signal Processing, by Oppenheim and Schafer, Prentice-Hall, Englewood Cliffs, NJ, 1975.





