The SMOOTH and MEDIAN functions are used to smooth images.

Images may be rapidly smoothed with the SMOOTH function. SMOOTH performs equally weighted smoothing using a square neighborhood of a given odd width. If A is an image of any type or size, the statement:

TVSCL, SMOOTH(A, 3)

displays the result of smoothing the image A with a 3-by-3 boxcar average. Smoothing with the triangular kernel:

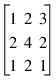
which approximates a two-dimensional triangle is easily implemented using the CONVOL function by the statement:

TVSCL, CONVOL(A,[[1,2,1],[2,4,2],[1,2,1]])

The first parameter, A, in the CONVOL function call, usually an image, is convolved with the second parameter, usually a much smaller kernel array of weights. The second parameter:

[[1,2,1],[2,4,2],[1,2,1]]

is the notation for a 3-by-3 array containing the kernel. The bracket [] symbols are the array concatenation operators. Elements between the brackets, which may be scalars, vectors or arrays, are concatenated.

This technique may be used for other types of smoothing, interpolation, or differentiation by changing the size and weights of the kernel parameter.

Median smoothing is a useful technique that is similar to mean smoothing as it is implemented by the SMOOTH function, except that the value of each pixel is replaced by the median of the N-by-N neighborhood rather than by the average.

Median smoothing, unlike mean smoothing, does not blur edges or features whose size is larger than the neighborhood. Also, median smoothing eliminates, without spreading, “salt and pepper” noise (isolated pixels containing extreme values). Median smoothing is implemented with the MEDIAN function:

TVSCL, MEDIAN(A, 3)

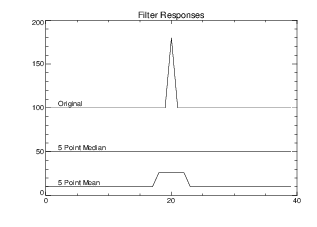
Figure 6-2: Median Smoothing shows the effect of median and mean filters on a one-dimensional vector containing an impulse step function. Notice how the impulse is eliminated by the median filter rather than spread over the neighborhood of the filter as it is in the mean filter.