Introduction
The routines in this chapter assume the time series does not contain any missing observations. If missing values are present, they should be set to NaN (see the routine MACHINE), and the routine will return an appropriate error message. To enable fitting of the model, the missing values must be replaced by appropriate estimates.
General Methodology
A major component of the model identification step concerns determining if a given time series is stationary. The sample correlation functions computed by routines AUTOCORRELATION Function, and PARTIAL_AC Function may be used to diagnose the presence of nonstationarity in the data, as well as to indicate the type of transformation1 require to induce stationarity. The family of power transformations provided by routine BOXCOXTRANS Function coupled with the ability to difference the transformed data using routine DIFFERENCE Function affords a convenient method of transforming a wide class of nonstationary time series to stationarity.
The “raw” data, transformed data, and sample correlation functions also provide insight into the nature of the underlying model. Typically, this information is displayed in graphical form via time series plots, plots of the lagged data, and various correlation function plots.
The observed time series may also be compared with time series generated from various theoretical models to help identify possible candidates for model fitting. The routine RANDOM_ARMA may be used to generate a time series according to a specified autoregressive moving average model.
Time Domain Methodology
Once the data are transformed to stationarity, a tentative model in the time domain is often proposed and parameter estimation1, diagnostic checking and forecasting are performed.
ARIMA Model (Autoregressive Integrated Moving Average)
A small, yet comprehensive, class of stationary time-series models consists of the nonseasonal ARMA processes defined by:
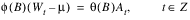
where Z = {..., −2, −1, 0, 1, 2, ...} denotes the set of integers, B is the backward shift operator defined by BkWt = Wt−k, μ is the mean of Wt, and the following equations are true:
φ(B) = 1 − φ1B − φ2B2 − ... − φpBp, p ≥ 0
θ(B) = 1 − θ1B − θ2B2 − ... − θqBq, q ≥ 0
The model is of order (p, q) and is referred to as an ARMA (p, q) model.
An equivalent version of the ARMA (p, q) model is given by:
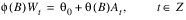
where θ0 is an overall constant defined by the following:
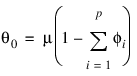
See Box and Jenkins (1976, pp. 92−93) for a discussion of the meaning and usefulness of the overall constant.
If the “raw” data, {Zt}, are homogeneous and nonstationary, then differencing using the DIFFERENCE Function induces stationarity, and the model is called ARIMA (AutoRegressive Integrated Moving Average). Parameter estimation is performed on the stationary time series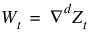 
, where 
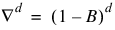is the backward difference operator with period 1 and order d, d > 0.
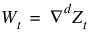, where 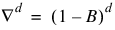is the backward difference operator with period 1 and order d, d > 0.Typically, the method of moments includes keyword Moments in a call to the ARMA Function for preliminary parameter estimates. These estimates can be used as initial values into the least-squares procedure by including keyword Lsq in a call to function ARMA. Other initial estimates provided by the user can be used. The least-squares procedure can be used to compute conditional or unconditional least-squares estimates of the parameters, depending on the choice of the backcasting length.
