FMINV Function
Minimizes a function f(x) of n variables using a quasi-Newton method.
Usage
result = FMINV(f, n)
Input Parameters
f—Scalar string specifying a user-supplied function to evaluate the function to be minimized. The f function accepts the following parameter and returns the computed function value at the point:
n—Number of variables.
Returned Value
result—The minimum point x of the function. If no value can be computed, NaN is returned.
Input Keywords
Double—If present and nonzero, double precision is used.
XGuess—Array with n components containing an initial guess of the computed solution. Default: XGuess (*) = 0
Grad—Scalar string specifying a user-supplied function to compute the gradient. This function accepts the following parameter and returns the computed gradient at the point:
XScale—Array with n components containing the scaling vector for the variables. Keyword XScale is used mainly in scaling the gradient and the distance between two points. See keywords Tol_Grad and Tol_Step for more detail. Default: XScale (*) = 1.0
FScale—Scalar containing the function scaling. Keyword Fscale is used mainly in scaling the gradient. See keyword Tol_Grad for more detail. Default: FScale = 1.0
Tol_Grad—Scaled gradient tolerance.
The ith component of the scaled gradient at x is calculated as:
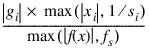
where:
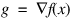
s = XScale, and fs = FScale. Default: Tol_Grad = ε1/2 (ε1/3 in double) where ε is the machine precision
Tol_Step—Scaled step tolerance.
The ith component of the scaled step between two points x and y is computed as:
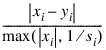
where s = XScale. Default: Tol_Step = ε 2/3
Tol_Rfcn—Relative function tolerance. Default:
Tol_Rfcn = max(10–10, ε 2/3), max(10–20, ε 2/3) in double
Tol_Rfcn = max(10–10, ε 2/3), max(10–20, ε 2/3) in double
Max_Step—Maximum allowable step size. Default: Max_Step = 1000max(ε1, ε2), where:
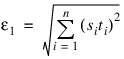
ε2 = || s ||2, s = XScale, and t = XGuess
N_Digit—Number of good digits in function. Default: machine dependent
Itmax—Maximum number of iterations. Default: Itmax = 100
Max_Evals—Maximum number of function evaluations. Default: Max_Evals = 400
Max_Grad—Maximum number of gradient evaluations. Default: Max_Grad = 400
Ihess—Hessian initialization parameter. If Ihess is zero, the Hessian is initialized to the identity matrix; otherwise, it is initialized to a diagonal matrix containing max ( f (t), fs) * si on the diagonal, where t = XGuess, fs = FScale, and s = XScale. Default: Ihess = 0
Output Keywords
FValue—Name of a variable into which the value of the function at the computed solution is stored.
Discussion
Function FMINV uses a quasi-Newton method to find the minimum of a function f (x) of n variables. The problem is stated below:
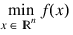
Given a starting point xc, the search direction is computed according to the formula:
d = –B–1gc
where B is a positive definite approximation of the Hessian and gc is the gradient evaluated at xc.
A line search is then used to find a new point:
xn = xc + λ d, λ > 0
such that:
f(xn) ≤ f(xc) α gTd
where 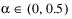 .
.
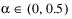 .
. Finally, the optimality condition:
|| g(x) || ≤ ε
is checked, where ε is a gradient tolerance.
When optimality is not achieved, B is updated according to the BFGS formula:
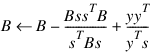
where s = xn – xc and y = gn – gc. Another search direction is then computed to begin the next iteration. For more details, see Dennis and Schnabel (1983, Appendix A).
In this implementation, the first stopping criterion for FMINV occurs when the norm of the gradient is less than the given gradient tolerance Tol_Grad. The second stopping criterion for FMINV occurs when the scaled distance between the last two steps is less than the step tolerance Tol_Step.
Since by default, a finite-difference method is used to estimate the gradient for some single-precision calculations, an inaccurate estimate of the gradient may cause the algorithm to terminate at a noncritical point. In such cases, high-precision arithmetic is recommended or keyword Grad is used to provide more accurate gradient evaluation.
Example 1
The function f(x) = 100 (x2 – x12)2 + (1 – x1)2 is minimized.
.RUN
; Define the function.
FUNCTION f, x
xn = x
xn(0) = x(1) - x(0)^2
xn(1) = 1 - x(0)
RETURN, 100 * xn(0)^2 + xn(1)^2
END
; Call FMINV to compute the minimum.
xmin = FMINV('f', 2); Output the solution.
PM, xmin, Title = 'Solution:'
; PV-WAVE prints the following:
; Solution:
; 0.999986
; 0.999971
PM, f(xmin), Title = 'Function value:'
; PV-WAVE prints the following:
; Function value:
; 2.09543e-10
Example 2
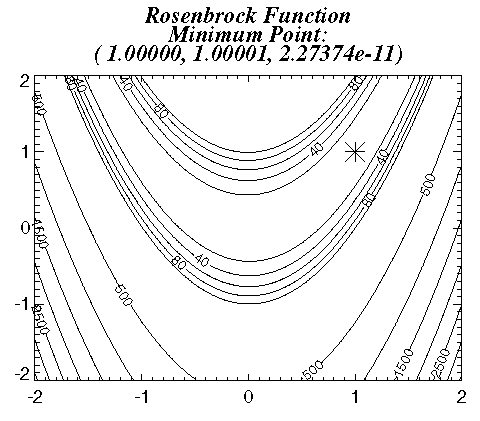
The function f(x) = 100 (x2 – x12)2 + (1 – x1)2 is minimized with the initial guess x = ( –1.2, 1.0). In the following plot, the asterisk marks the minimum. The results are shown in Figure 9-3: Rosenbrock Function Plot.
.RUN
; Define the function.
FUNCTION f, x
xn = x
xn(0) = x(1) - x(0)^2
xn(1) = 1 - x(0)
RETURN, 100 * xn(0)^2 + xn(1)^2
END
.RUN
; Define the gradient function.
FUNCTION grad, x
g = x
g(0) = -400 * (x(1) - x(0)^2) * x(0) - 2 * (1 - x(0))
g(1) = 200 * (x(1) - x(0)^2)
RETURN, g
END
; Call FMINV with the gradient function, an initial guess, and a
; scaled gradient tolerance.
xmin = FMINV('f', 2, grad = 'grad', XGuess = [-1.2, 1.0], $Tol_Grad = .0001)
x = 4 * FINDGEN(100)/99 - 2
y = x
surf = FLTARR(100, 100)
; Evaluate function f on 100 by 100 grid for use in CONTOUR.
FOR i=0L, 99 DO FOR j=0L, 99 do $
surf(i, j) = f([x(i), y(j)])
str = '(' + STRCOMPRESS(xmin(0)) + ',' + $STRCOMPRESS(xmin(1)) + ',' + STRCOMPRESS(f(xmin)) + ')'
!P.Charsize = 1.5
; Call CONTOUR. Customize the contour plot, including the
; title of the plot.
CONTOUR, surf, x, y, Levels = [20*FINDGEN(6), $
500 + FINDGEN(7)*500], /C_Annotation, $
Title='!18Rosenbrock Function!C' + 'Minimum Point:!C' + $
str, Position = [.1, .1, .8, .8]
; Plot the solution as an asterisk.
OPLOT, [xmin(0)], [xmin(1)], Psym = 2, Symsize = 2
 |
Informational Errors
MATH_STEP_TOLERANCE—Scaled step tolerance satisfied. Current point may be an approximate local solution, but it is also possible that the algorithm is making very slow progress and is not near a solution or that Tol_Step is too big.
Warning Errors
MATH_REL_FCN_TOLERANCE—Relative function convergence. Both the actual and predicted relative reductions in the function are less than or equal to the relative function convergence tolerance.
MATH_TOO_MANY_ITN—Maximum number of iterations exceeded.
MATH_TOO_MANY_FCN_EVAL—Maximum number of function evaluations exceeded.
MATH_TOO_MANY_GRAD_EVAL—Maximum number of gradient evaluations exceeded.
MATH_UNBOUNDED—Five consecutive steps have been taken with the maximum step length.
MATH_NO_FURTHER_PROGRESS—Last global step failed to locate a point lower than the current x value.
Fatal Errors
MATH_FALSE_CONVERGENCE—Iterates appear to converge to a noncritical point. It is possible that incorrect gradient information is used, or the function is discontinuous, or the other stopping tolerances are too tight.





