Segmented hyperedges
Describes hyperedge segments, their angles and operations, and provides a summary of the classes used to work with them.

Provides an overview of segmented hyperedges, and how they differ from standard hyperedges.

Describes segmented hyperedges, segment trees, and how to retrieve the segments of a hyperedge.

Defines the different angles of a hyperedge segment.

Describes the operations of hyperedge segments, and the methods used to work with them.
Overview
IlvHyperEdge is the base class for hyperedges. It is comparable to
IlvLinkImage, which is the base class for links.
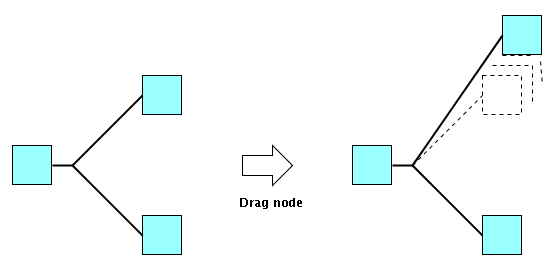
IlvHyperEdge draws a star-like shape from a center point of the hyperedge to the ends of the hyperedge.
For many applications, the star-like shape is inappropriate, because applications prefer specific shapes, such as a shape consisting of orthogonal segments. To create such shapes, use the class
IlvSegmentedHyperEdge, which is a subclass of
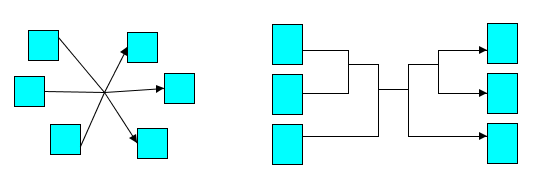
IlvHyperEdge. The following figure shows examples of
IlvHyperEdge (on the left) and
IlvSegmentedHyperEdge (on the right).
Hyperedge and segmented hyperedge
Hyperedge segments
An
IlvSegmentedHyperEdge object has a shape that consists of line segments. The line segments form branches that connect all hyperedge ends. Therefore, the segments can be connected to other segments and can be connected to hyperedge ends at a node. We call a segment
incident to a node an
end segment, and the other segments the
inner segments. The segments of a hyperedge form an unrooted, undirected segment tree.
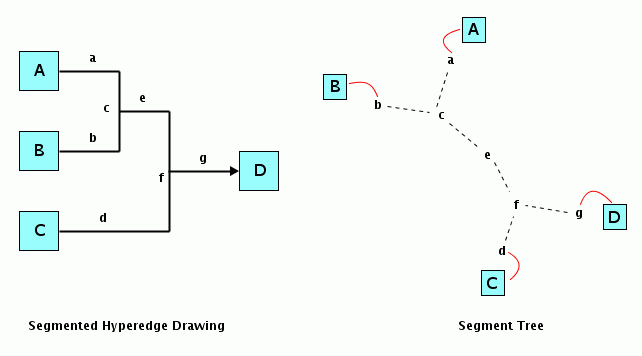
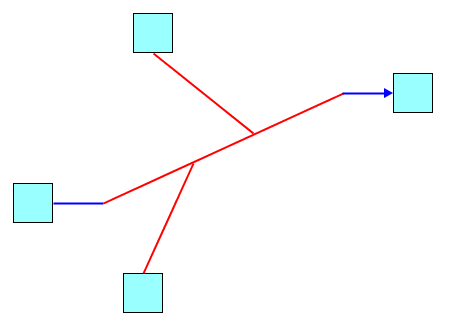
A segmented hyperedge with its segment tree
In the figures above:

The dashed lines indicate the segments that are incident.

The red lines indicate which segments are connected to end nodes.

The segments a, b, d, and g are end segments; the segments c, e, and f are inner segments.
You may be surprised that the segment tree is undirected, even though the hyperedge may be directed. The direction of the hyperedge comes from the fact that arrow heads are drawn at certain end points. This direction is irrelevant for the segment tree; that is, there is no root of the segment tree, but each segment has several (or 0) incident segments. By starting at an arbitrary segment, an algorithm can traverse all incident segments recursively without running into a cycle. Therefore it is an unrooted, undirected segment tree.
A segment is implemented by the inner class
IlvSegmentedHyperEdge.Segment. To retrieve all segments of a hyperedge, make the call shown in the following code example.
Retrieving all segments of a hyperedge
IlvSegmentedHyperEdge seghyperedge = ...
Iterator iterator = seghyperedge.getSegments();
while (iterator.hasNext()) {
IlvSegmentedHyperEdge.Segment segment =
(IlvSegmentedHyperEdge.Segment)iterator.next();
...
}
The API of IlvSegmentedHyperEdge.Segment includes the methods listed in the following table.
Methods of IlvSegmentedHyperEdge.Segment
Method | Description |
| Returns the hyperedge that owns the segment. |
| Returns the hyperedge ends of the segment if it is an end segment. If it returns an empty array, the segment is an inner segment. |
| Returns the number of incident segments. |
| Returns the incident segment with index i. The index of incident segments starts at 0. |
| Tests whether two segments are incident. |
If two segments A and B are connected, then A will have B as incident segment and B will have A as incident segment. This allows traversal of the incident segments in any direction. To avoid running into a loop, you only have to make sure that you do not visit the segment again where you immediately came from. The method in the following code example illustrates this concept.
Method for traversal of incident segments in any direction
public void visit(IlvSegmentedHyperEdge.Segment segment,
IlvSegmentedHyperEdge.Segment cameFrom)
{
...
int n = segment.getIncidentSegmentsCount();
for (int i = 0; i < n; i++) {
IlvSegmentedHyperEdge.Segment childSegment =
segment.getIncidentSegment(i);
if (childSegment != cameFrom)
visit(childSegment, segment);
}
}
...
// visit all segments reachable from startSegment
visit(startSegment, null);
The angle of a segment
Many applications use orthogonal segments, that is, the angle of a segment can be 0 degrees (horizontal) or 90 degrees (vertical).
IlvSegmentedHyperEdge supports orthogonal segments and also segments with a different fixed angle. It also supports segments with variable angle.
Fixed angle or variable angle
A segment with fixed angle always keeps this angle. When
incident segments or end nodes are moved or dragged, a segment will become longer or shorter to stay visually connected, but it will not change its angle. This is shown in figures
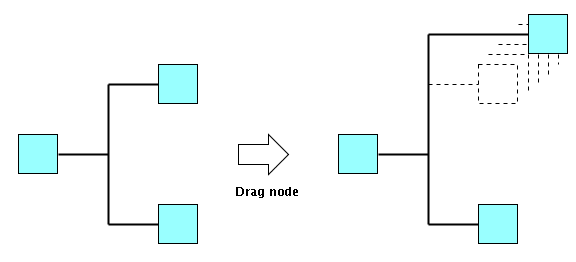
Orthogonal segments with fixed angle and
Segments with fixed angle of 45 degrees.
Orthogonal segments with fixed angle
In figure
Orthogonal segments with fixed angle, when end nodes are dragged, the segments remain orthogonal. They only get longer.
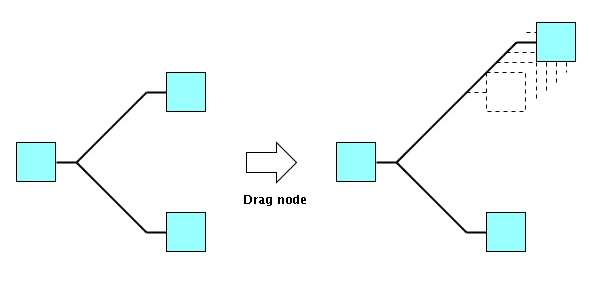
Segments with fixed angle of 45 degrees
In figure
Segments with fixed angle of 45 degrees, when end nodes are dragged, the segments don't change their angle. They only get longer.
A segment with variable angle always adapts the angle to the situation automatically. When incident segments or end nodes are moved or dragged, the segment will change its angle. This is shown in figure
Segments with variable angle.
Segments with variable angle
In figure
Segments with variable angle, when end nodes are dragged, the segments change the angle.
Whether a segment has a variable angle or a fixed angle depends on how the segment was created. This is described later, in
Segment operations.
To test whether a segment has a variable or a fixed angle, call the method:
segment.isVariable()
The angle of a segment is always given in degrees between 0 and 180, where 0 means horizontal and 90 means vertical.
To query the angle of the segment, call the method:
segment.getAngle()
Constraints of variable and fixed angle segments
In the segment tree, segments of fixed or variable angle can be incident, but there are some constraints:

A segment with fixed angle can be incident to any number of other segments with fixed or variable angle.

A segment with fixed angle cannot be incident to a segment with the same fixed angle. For example, a horizontal segment cannot be incident to another horizontal segment. If the shape of the hyperedge is orthogonal, then horizontal segments will be incident to vertical segments and vertical segments will be incident to horizontal segments. Segments with the same angle are called
colinear. See
isColinear. For mathematical reasons, it is required that the angle differs at least by 1 degree.

A segment with fixed angle can only be connected to at most one hyperedge end (
getEnds() returns an array with at most 1 end).

A segment with variable angle can be incident to any number of other segments with variable angle.

A segment with variable angle usually starts or ends at a node or at a segment. In the latter case, it is said to be
terminated by a segment. The terminating segments of a segment with variable angle can have a fixed angle or a variable angle.

A segment with variable angle can be connected to 0, 1, or 2 hyperedge ends (
getEnds() returns an array with at most 2 ends).
Hyperedge consisting of segments of fixed and variable angle

Segments with fixed angle are blue.

Segments with variable angle are red.

The long red segment in the middle of the figure is terminated by segments of fixed angle.
Segment operations
This section describes segment operations and their effects.
Complete or incomplete segment tree
Each end of a hyperedge has a segment that is directly incident to the hyperedge end. You can obtain this segment by calling:
seghyperedge.getEndSegment(hyperedgeEnd);
The segment tree is complete, if each end of the hyperedge is reachable from each other end through a segment traversal. See the method
visit in section
Method for traversal of incident segments in any direction.
If this is not the case, the segment tree is incomplete. For example, you have a disconnected forest of segment trees.
To test whether a segment tree is complete, call:
seghyperedge.isSegmentSetComplete();
Hyperedges with incomplete segment trees can be displayed. Incomplete segment trees look wrong when displayed. They do not convey information on which nodes are connected by the hyperedge. Therefore, you are usually interested only in complete segment trees.
The API of
IlvSegmentedHyperEdge is flexible enough to allow incomplete segment trees, which simplifies the task of restructuring the segments of a hyperedge.
The segment tree can be made incomplete temporarily, but for the final drawing you are recommended to make the segment tree complete.
Therefore, it is necessary to distinguish between primitive segment operations and safe segment operations.
Primitive operations can make the segment tree incomplete.
Safe segment operations, when applied to a complete segment tree, result in a complete segment tree.
Primitive segment operations
The API on
IlvSegmentedHyperEdge.Segment allows you to query the information of the segment, but not to manipulate the segments. The manipulation must be done by the API on the hyperedge itself. Any manipulation of the segment tree may change the bounding box of the hyperedge. Therefore, an
applyToObject session is usually necessary.
The following primitive segment operations allow you to change the segment tree so that it becomes incomplete. The API of
IlvSegmentedHyperEdge includes the methods listed in the following table.
Methods of IlvSegmentedHyperEdge for making the segment tree incomplete
Method | Description |
| Creates a new segment that is incident to the hyperedge end. The new segment has a fixed angle. |
| Creates a new segment that is incident to the hyperedge end. The new segment has a variable angle. As long as the segment is not terminated by any other segment, it uses the point (x, y) as the other termination point of the segment. |
| Creates a new segment that is incident to both hyperedge ends. The new segment has a variable angle. |
| Creates a new segment that is incident to the existing segment. The new segment has a fixed angle. The input point (x,y) determines the position of the segment. |
| Creates a new segment that is incident to the existing segment. The new segment has a variable angle. The input points (x1,y1) and (x2,y2) determine the start and end coordinates of the new segment. |
| Removes a segment from the segment tree. This makes the segment tree incomplete. Returns the segments that were formerly incident to the removed segment. |
| Connects two segments so that they become incident. It is not possible to connect segments in a way that would form a cycle in the segment tree. The constraints on variable and fixed angle segments must be observed. |
| Disconnects two segments so that they are no longer incident. This makes the segment tree incomplete. |
| Tests whether two segments are connected. |
Safe segment operations
When hyperedge ends are added to or removed from the hyperedge, the segment tree must change to remain complete. The hyperedge has an autoconnect mode that does this automatically.
The following code example shows how to keep the segment tree complete.
Keeping the segment tree complete
IlvSegmentedHyperEdge seghyperedge = ...
seghyperedge.setAutoConnect(true);
// ... this will add segments automatically as necessary
seghyperedge.addFrom(node);
seghyperedge.addTo(node);
// ... now the segment tree is complete
// seghyperedge.isSegmentSetComplete() == true
The following code example shows how to make the segment tree incomplete.
Making the segment tree incomplete
IlvSegmentedHyperEdge seghyperedge = ...
seghyperedge.setAutoConnect(false);
// ... this will not add any segments automatically
seghyperedge.addFrom(node);
seghyperedge.addTo(node);
// ... now the segment tree is incomplete, since the new hyperedge ends
// are not connected ...
// seghyperedge.isSegmentSetComplete() == false
The autoconnect mode is enabled by default.
The API of
IlvSegmentedHyperEdge contains further operations that keep the segment tree complete.
Methods of IlvSegmentedHyperEdge for keeping the segment tree complete
Method | Description |
| Variants of this operation exist. They split a segment into a sequence of segments, that is, a bend will occur at the position where the segment was split. See the Java™ API reference manual for information about the variants. |
| This is the inverse of the split operation. It joins two segments, so that instead of two, only one segment is used. This operation removes a bend in the shape of the hyperedge. |
| Changes the angle of the input segment. If the input segment is connected, this will work only if no incident segment is colinear with the new angle. |
| Changes the angle of the segment that is incident to the input hyperedge end. It reorganizes the segment tree so that the desired angle is possible for the segment at the input end. |
See
IlvSegmentedHyperEdge for more information on segmented hyperedges.
Copyright © 2018, Rogue Wave Software, Inc. All Rights Reserved.