Map projections
Tells you all about map projections.

Describes map projections and gives diagrams illustrating the different categories.

Lists the predefined projections available with information on the category and characteristics of each projection.

Describes projection methods and parameters.

Shows how to extend the
JViews Maps projection package with your own projections.
Introducing map projections
A map is a projected representation of the Earth, or part of it, on a flat surface, which can be a piece of paper or a computer screen. Since the Earth has an ellipsoidal shape, it is best represented as a “globe”, and attempts to portray it by projecting its points onto a flat surface always result in some form of distortion in the regions that are far from the projection center. In other words, it is impossible to faithfully represent all the properties of the Earth, such as distances, shapes, and directions, on the same map. To minimize distortion, many different types of projections have been developed over the years. While certain projections preserve distances, others maintain shapes or angles. When creating a map, you have to choose the projection system that is best suited to the area to be represented or to the particular interests that your map application is designed for.
Projections can be classified into three main categories:
Projections can also be:
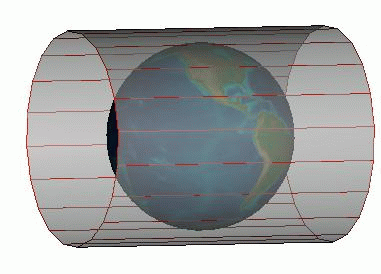
Cylindrical projections
A cylindrical projection is obtained by wrapping a large, flat plane around the globe to form a cylinder. In the following figure, the cylinder is tangential to the equator. The closer the zone of tangency the less the distortion.
A cylindrical projection (1)
The position of the cylinder can be changed. For example, in a transverse cylindrical projection, the cylinder is tangential to a meridian.
A cylindrical projection (2)
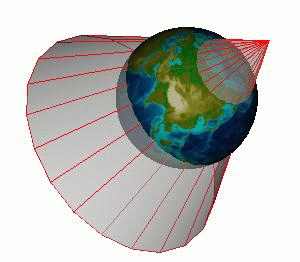
Conic projections
A conic projection transfers the image of the globe to a cone that forms either a secant or a tangent with the surface of the Earth.
Examples of conic projections
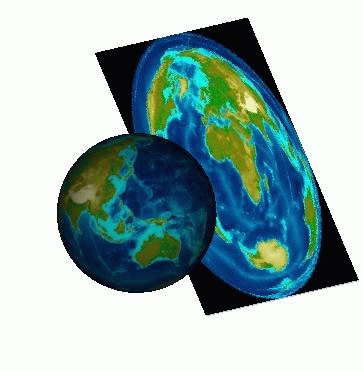
Azimuthal projections
With azimuthal projections, also called planar projections, the spherical globe is projected onto a flat surface.
An azimuthal projection
Equal area or conformal projections
All map projections show some kind of distortion in the areas that are far from the projection center. Depending on the kind of projection used, the distortion may be of angle, area, shape, size, distance, or scale. In this respect, projections fall into two main categories, Equal Area and Conformal.

Equal area projections maintain a true ratio between the various areas represented on the map.

Conformal projections preserve angles, and locally also preserve shapes.
Other projections have properties that are worth noting, such as maintaining the distances measured from the center of the projection (azimuthal equidistant projection). Others offer a good compromise between angular distortion and distortion of the area.
Projections should therefore be configured and selected according to the areas to be represented (for example, it is impossible to represent the polar regions with the Mercator projection) and the domains they apply to (navigational or air-route applications, small-scale or large-scale maps, and so on). Navigational applications, for example, generally use conformal projections.
For more information on map projections, refer to these books:
 Map Projections - A Working Manual
Map Projections - A Working Manual (Snyder, 1987)
 An Album of Map Projection
An Album of Map Projections (Snyder and Voxland, 1989)
Predefined projections
The following table provides a list of the predefined projections that are available.
Projection name | Classification | Conformal | Equal Area |
Albers Equal Area | Conic | No | Yes |
Azimuthal Equidistant Projection | Azimuthal | No | No |
Cassini | Cylindrical | No | No |
Cylindrical Equal Area also known as: • Lambert Cylindrical Equal Area • Behrmann • Gall Orthographic • Peters | Cylindrical | No | Yes |
Eckert IV | Pseudo Cylindrical | No | Yes |
Eckert VI | Pseudo Cylindrical | No | Yes |
Equidistant Cylindrical also known as: • EquiRectangular • Plate Carré | Cylindrical | No | No |
French Lambert | Conic | Yes | No |
Geographic | N/A | - | - |
Gnomonic | Azimuthal | No | No |
Lambert Azimuthal Equal Area also known as: • Lorgna • Zenithal Equal Area • Zenithal Equivalent | Azimuthal | No | Yes |
Lambert Conformal Conic | Conic | Yes | No |
Lambert Equal Area Conic | Conic | No | Yes |
Mercator also known as: • Wright | Cylindrical | Yes | No |
Miller Cylindrical | Cylindrical | No | No |
Mollweide also known as: • Homolographic • Babinet • Elliptical | Pseudo Cylindrical | No | Yes |
Oblique Mercator also known as: • Hotine Oblique Mercator | Cylindrical | Yes | No |
Orthographic | Azimuthal | No | No |
Polyconic | Polyconic | No | No |
Robinson | Pseudo Cylindrical | No | No |
Sinusoidal also known as: • Sanson-Flamsteed • Mercator Equal-Area | Pseudo Cylindrical | No | Yes |
Stereographic | Azimuthal | Yes | No |
Transverse Mercator also known as: • Gauss Conformal • Gauss-Krüger • Transverse Cylindrical Orthomorphic | Cylindrical | Yes | No |
Universal Polar Stereographic | Azimuthal | Yes | No |
Universal Transverse Mercator | Cylindrical | Yes | No |
Wagner IV | Pseudo Cylindrical | No | Yes |
Projection methods and parameters
Forward and inverse methods
Projections are implemented using the forward and inverse methods:

The
forward method converts a geographic point, defined by a longitude and a latitude, to its Cartesian coordinates.

The
inverse method converts Cartesian coordinates to a latitude and a longitude.
These methods can throw exceptions of two different types that both inherit from the class IlvProjectionException:

When trying to perform a forward projection on a nonspherical ellipsoid when the projection does not support nonspherical ellipsoids (
IlsEquidistantCylindricalProjection for example).

When trying to inverse a projection that cannot be reversed.
To know whether these features are implemented in the projection you are using, use the methods
isEllipsoidEnabled and
isInverseEnabled.
Projection parameters
You can set the following parameters for a projection:

The ellipsoid that specifies the figure of the Earth.
For more information on ellipsoids, refer to section
Ellipsoids.
Each projection is associated with an ellipsoid. By default, most of the projections use the ellipsoid
SPHERE. Only some specific projections, such as the Universal Transverse Mercator or the Universal Polar Stereographic, use a nonspherical ellipsoid by default.
You will obtain more accurate projections using an appropriate ellipsoid, especially with large scale maps. Note, however, that computations are more complex and slower than when using a sphere.
To specify the ellipsoid you want to use for a projection, use the method
setEllipsoid.
IlvProjection projection = new IlvMercatorProjection();
projection.setEllipsoid(IlvEllipsoid.WGS84);
You can either use a static member of the class
IlvEllipsoid, which defines a number of commonly used ellipsoids, or create your own ellipsoid as explained in the section
Defining new ellipsoids. You can also use one of the predefined ellipsoids listed in the section
Predefined ellipsoids.

The unit converter that specifies the measurement unit in which Cartesian coordinates should be expressed.

The central meridian and the central parallel of the projection.
These parameters can be set with the
setLLCenter method. Projections produce less distortion near their center.

The offset applied to the Cartesian coordinates, also called false easting and false northing. These parameters can be set with the method
setXYOffset. The offset can be used in conjunction with the unit converters to control the range of projected coordinates for a region. For example, the range of the region may be set so that the region fits into a square of size 200 x 200. In
JViews Maps applications, the range of the data is not an issue, since a transformer can be automatically applied to fit all the graphics contained in an
IlvManager into a window. Therefore, false easting and false northing are mainly used to adapt a projection to geographic data that has already been projected using a Cartesian offset.
You can also:

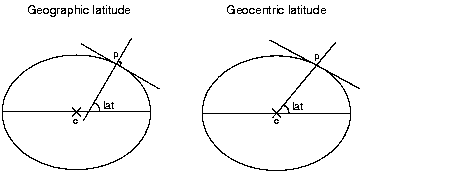
Specify whether the coordinates are geodetic (the default value) or geocentric using the
setGeocentric method.
The geocentric latitude of a point is defined by the angle formed by a line joining the point to the center of the Earth and the equatorial plane, whereas the geodetic (or geographic) latitude of a point is defined by the angle formed by the vertical line passing through this point and the equatorial plane. The two values differ since the Earth is not exactly a sphere but rather an ellipsoid. Both latitudes are related through the relation tan phiG = (1 - e ^ 2) tan phi where e is the eccentricity of the ellipsoid used to model the shape of the Earth.
If an application handles geocentric data, this parameter must be set. Most of the available cartographic data available is expressed with geographic latitudes.

Specify whether the projection uses longitude reduction, that is, forces longitude to be in the range
[-PI;PI] or accepts any longitude, using the method
setUsingLongitudeReduction.
The above parameters are common to all the projections. They can be set with the API of the class IlvProjection, which is the base class of all the projections in the package. Some projections have additional specific parameters. For example, secant latitudes can be specified for a conic projection, or the latitude of the true scale can be specified for most cylindrical projections. For more information, refer to the documentation of the API for each projection.
Projection utilities
The class
IlvProjectionUtil provides conversion utilities to convert radians to degrees and degrees to radians.
Creating a new projection
The procedure is based on an example that implements a simplified version of the Mercator projection. The complete code for this example can be found in the following file:
Defining a new projection class
The complete source code of the examples presented in the next sections can be found in the following file:
Mercator example.
2. Your projection class must extend the class
IlvProjection, which is the base class for all the projections in the package.
import ilog.views.maps.projection.*;
import ilog.views.maps.*;
class MercatorProjection
extends IlvProjection
Writing the constructor

You must call the constructor of the superclass
IlvProjection.
MercatorProjection()
{
super(true, true, IlvProjection.CONFORMAL);
}
This constructor takes the following three arguments:

The first argument is a
boolean value specifying whether the projection supports nonspherical ellipsoids. In our example, this argument is set to
true since the projection supports the equations for these ellipsoids.

The second argument is a
boolean value indicating whether the projection supports an inverse method. In our example, this argument is set to
true since the projection supports an inverse method.

The third argument is an
int value that indicates the geometric properties of the projection. In our example, this argument is
IlvProjection.CONFORMAL since the Mercator projection is conformal.
Writing the Forward Projection
Before writing the forward() method for the Mercator projection, you must be familiar with the IlvProjection.forward() method.
The IlvProjection.forward() public method is called by the user to project data. This method prepares data for projection computation and scales it appropriately. It then redirects the calls to either one of the eforward or sForward protected methods which are defined in the projection subclass (the Mercator class in our example). In most cases, the forward method should not be overridden.
The
forward method has the following effects:
1. It adjusts the latitude, if the coordinates are geocentric.
2. It adjusts the longitude to the central meridian of the projection.
3. It adjusts the longitude to the range [-PI;PI], if longitude reduction is used (the default value).
4. It calls either the method
sForward or
eForward depending on whether the Earth is represented as a sphere or as an ellipsoid.
5. Adjusts the projected data to the dimensions of the ellipsoid and to the Cartesian offset, and converts it to the selected measurement unit.
Projecting data from a sphere
The sforward() protected method implements the projection of a sphere.
Since the appropriate scaling is actually carried out by the method IlvProjection.forward(), the sForward() method always assumes that the radius of the sphere is 1.
In the example, the Mercator projection is the projection of a sphere onto a cylinder that is tangential to the equator. The x coordinate is equal to the longitude because it is assumed that the radius of the sphere is 1, and longitude is expressed in radians. In this case, you do not need to change the x value of ll.
Because the Mercator projection cannot show regions near the poles, the exception
IlvToleranceConditionException is thrown if the latitude is too close to
PI/2.

Apply the equation to compute the
y -coordinate of the projected data.
protected void sForward(IlvCoordinate ll)
throws IlvToleranceConditionException
{
if (Math.abs(Math.abs(ll.y) - Math.PI / 2D) <= 1e-10D)
throw new IlvToleranceConditionException();
ll.y = Math.log(Math.tan(Math.PI / 4D + .5D * ll.y));
}
Projecting data from an ellipsoid
The eforward() protected method is called by the IlvProjection.forward() method if data is projected from a nonspherical ellipsoid.

It is not necessary for you to implement the
eForward() method for your projection. If you are projecting data from a nonspherical ellipsoid and if the projection you are using does not support this kind of ellipsoid, the
forward() method will throw the exception
IlvUnsupportedProjectionFeature. In this case, you can use any spherical ellipsoid or create an equivalent sphere using the appropriate conversion methods of the class
IlvEllipsoid.
The eForward() method is slightly more complex than the sForward() method although their formulas are equivalent if getEllipsoid().getE() returns 0.
protected void eForward(IlvCoordinate ll)
throws IlvToleranceConditionException
{
if (Math.abs(Math.abs(ll.y) - Math.PI / 2D) <= 1e-10D)
throw new IlvToleranceConditionException();
double e = Math.sqrt(getEllipsoid().getES());
double sinphi = e * Math.sin(ll.y);
ll.y = Math.tan (.5D * (Math.PI/2D - ll.y)) /
Math.pow((1D - sinphi) / (1D + sinphi),
.5D * e);
ll.y = -Math.log(ll.y);
}
Writing the inverse projection
Before writing the
inverse() method for the Mercator projection, you should be familiar with the
inverse method.
The IlvProjection.inverse() method prepares the data for inversion and processes it for the appropriate offset. In most cases, you should not have to override the IlvProjection.inverse() method.
This method has the following effects:
1. Suppresses the offset produced by the Cartesian coordinates and converts these coordinates to meters.
2. Reverts the coordinates to their geographic values and applies them to a standard ellipsoid with a semi-major axis of value 1.
3. Calls the method sInverse() or eInverse() depending on whether the ellipsoid is a sphere or not.
4. Adds the value of the central meridian to the longitude and adjusts the longitude to the range [-PI;PI] if longitude reduction is used (the default value).
5. Converts the latitude if the coordinates are geocentric.
Inverse projection onto a sphere
The inverse projection onto a sphere is performed via the
sInverse method.
1. It is not necessary for you to implement the
sInverse() method. If you call the
IlvProjection.inverse() method for a projection that does not support the
inverse() method, the exception
IlvUnsupportedProjectionFeature will be thrown.
2. The
sInverse() method can throw the exception
IlvToleranceConditionException like all the forward methods. But since the inverse equation of the Mercator projection is defined for all the possible values, this method does not throw any exceptions.
3. As with the sForward() method, the projection does not modify the x value, therefore, the inverse equation is applied only to the y value.
protected void sInverse(IlvCoordinate xy)
{
xy.y = Math.PI/2D - 2D * Math.atan(Math.exp(-xy.y));
}
Inverse projection onto an ellipsoid
The inverse projection onto an ellipsoid is performed via the
eInverse method.
This method assumes that the value of the semi-major axis of the ellipsoid is 1.

In the particular case of the Mercator projection, the implementation of this method is more complex for an ellipsoid than for a sphere. It requires iterations and might fail, since there is no simple analytical inverse equation of the Mercator projection from a nonspherical ellipsoid.
protected void eInverse(IlvCoordinate xy)
throws IlvToleranceConditionException
{
double ts = Math.exp(- xy.y);
double e = Math.sqrt(getEllipsoid().getES());
double eccnth = .5D * e;
double Phi = Math.PI/2D - 2D * Math.atan(ts);
int i = 15;
double dphi;
do {
double con = e * Math.sin (Phi);
dphi = Math.PI/2D - 2D * Math.atan(ts * Math.pow((1D - con) /
(1D + con), eccnth)) - Phi;
Phi += dphi;
} while ((Math.abs(dphi) > 1e-10D) && (--i != 0));
if (i <= 0)
throw new IlvToleranceConditionException("non-convergent inverse phi2");
xy.y = Phi;
}
Copyright © 2018, Rogue Wave Software, Inc. All Rights Reserved.