RWLeastSqSVDCalc
Class RWLeastSqSVDCalc employs singular value decomposition (SVD). The method solves the least squares problem by decomposing the regression matrix into the form 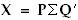 , where P is an
, where P is an 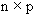 matrix consisting of p orthonormalized eigenvectors associated with the p largest eigenvalues of
matrix consisting of p orthonormalized eigenvectors associated with the p largest eigenvalues of 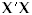 , Q is a
, Q is a  orthogonal matrix consisting of the orthonormalized eigenvectors of
orthogonal matrix consisting of the orthonormalized eigenvectors of 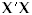 , and Σ = diag(σ1, σ2, ... , σp) is a
, and Σ = diag(σ1, σ2, ... , σp) is a  diagonal matrix of singular values of X. This singular value decomposition of X is used to solve the equation in Calculation Methods for Linear Regression .
diagonal matrix of singular values of X. This singular value decomposition of X is used to solve the equation in Calculation Methods for Linear Regression .
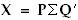 , where P is an
, where P is an 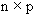 matrix consisting of p orthonormalized eigenvectors associated with the p largest eigenvalues of
matrix consisting of p orthonormalized eigenvectors associated with the p largest eigenvalues of 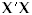 , Q is a
, Q is a  orthogonal matrix consisting of the orthonormalized eigenvectors of
orthogonal matrix consisting of the orthonormalized eigenvectors of 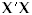 , and Σ = diag(σ1, σ2, ... , σp) is a
, and Σ = diag(σ1, σ2, ... , σp) is a  diagonal matrix of singular values of X. This singular value decomposition of X is used to solve the equation in Calculation Methods for Linear Regression .
diagonal matrix of singular values of X. This singular value decomposition of X is used to solve the equation in Calculation Methods for Linear Regression .Pros: | Works on matrices of less than full rank. Produces accurate results when X has full rank, but is highly ill-conditioned. |
Cons: | Slower than the straight QR technique described in RWLeastSqQRCalc. |





