Class RWLinearRegressionFTest
Suppose that we have the linear regression model:
Y = β0 + β1x1 + β2x2 + β3x3 + β4x4
and we want to test the hypothesis Ha:β2 = β4 = 0 and the hypothesis Hb:β1 = β3.
We can express each of these hypotheses in the matrix form Aβ = c, where β = [β0, β1, β2, β3, β4], c = 0,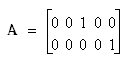 
for Ha, and A = [0 1 0 –1 0] for Hb.
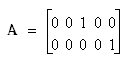for Ha, and A = [0 1 0 –1 0] for Hb.The RWLinearRegressionFTest class can be used for testing hypotheses of the above form Aβ = c, where β is the vector of p parameters for the linear regression model, A is a known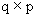 
matrix of rank q, and c is a known 
vector. The following is an example that tests both types of hypotheses.
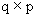matrix of rank q, and c is a known vector. The following is an example that tests both types of hypotheses.int main()
{
RWGenMat<double> predictorMatrix; // Predictor variable values
RWMathVec<double> observationVector; // Dependent variable values
double significanceLevel = .05;
if ( !getDataFromFile("crime.dat", predictorMatrix,
observationVector) )
{
return 0;
}
RWLinearRegression lr( predictorMatrix, observationVector );
RWLinearRegressionFTest FTest( lr );
// Test that B3 = B4.
RWGenMat<double> A( 1, lr.numParameters(), 0.0 );
RWMathVec<double> c( 1, 0.0 );
A(0,3) = 1.0;
A(0,4) = -1.0;
FTest.setHypothesis( A, c );
cout << "F Test for H0 B3 = B4\n" << endl;
cout << " F statistic value: " << FTest.FStatisticValue() <<
endl;
cout << " F statistic p-value: " << FTest.FStatisticPValue() <<
endl;
cout << " Critical value: " <<
FTest.criticalValue(significanceLevel) << '\n' << endl;
if ( FTest.reject(significanceLevel) )
{
cout << "Reject H0 at significance level " << significanceLevel
<< endl;
}
else
{
cout << "Fail to reject H0 at significance level " <<
significanceLevel << endl;
}
return 0;
}
