Logistic Regression
Logistic regression is used to model the relationship between a binary response variable and one or more predictor variables, which may be either discrete or continuous. Binary outcome data is common in medical applications. For example, the binary response variable might be whether or not a patient is alive five years after treatment for cancer or whether the patient has an adverse reaction to a new drug. As in multiple regression, we are interested in finding an appropriate combination of predictor variables to help explain the binary outcome.
Let Y be a dichotomous random variable denoting the outcome of some experiment, and let X = (x1, x2, ... , xp – 1) be a collection of predictor variables. Denote the conditional probability that the outcome is present by P(Y = 1|x) = π(x), where π(x) has the form:

If the xj are varied and the n values Y1,Y2, ... , Yn of Y are observed, we write:

The logistic regression problem is then to obtain an estimate of the vector:

As with multiple linear regression, the matrix: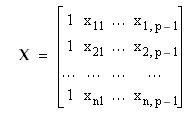
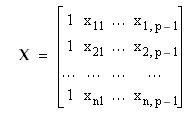
is called the regression matrix, while the matrix R, containing only the data for the predictor variables (matrix X without the leading column of 1s), is called the predictor data matrix.





