6.5 Tridiagonal Decompositions

The objects introduced in this next section will probably not find their way into general use; nevertheless, you may find it interesting to read how the server classes are implemented. The discussion is kept brief; for details refer to the Class Reference.

Many algorithms for computing an eigenvalue decomposition, including all the algorithms implemented in LAPACK.h++, do not find the eigenvalues of the symmetric matrix A directly. Instead, a tridiagonal decomposition:

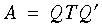
is computed, where Q is orthogonal and T symmetric and tridiagonal, and the algorithm works directly on the simpler matrix T. Once the eigenvalues and eigenvectors of T are known, it is a simple matter to obtain A's eigenvalue decomposition. The eigenvalues are the same, and the eigenvectors are obtained by premultiplying by Q.

The symmetric tridiagonal decomposition is encapsulated by a hierarchy of three classes, as shown in Table 8:

Table 8 -- Symmetric tridiagonal decomposition classes

The base eigenvalue server class contains one pure virtual function, decompose(const TDDecomp&). This function is required to compute the eigenvalue decomposition of the tridiagonal matrix within the decomposition; it is the only function that must be provided by each specific server. Since decompose uses the abstract base tridiagonal decomposition class, its code works equally well for dense or band decompositions.

When you ask a server for the decomposition of a matrix, the default base server computes the appropriate symmetric tridiagonal decomposition, uses decompose to do the computation for the tridiagonal matrix, and then transforms the results so that they apply to the original matrix. Of course, if you want to create a server that does not use tridiagonal decompositions, you can simply override the server's operator() functions directly.

©Copyright 1999, Rogue Wave Software, Inc.
Contact Rogue Wave about documentation or support issues.