3.5 Accessing Data

The matrix classes contain a number of member functions for accessing and modifying data. In this section, we describe these functions and give brief examples.

3.5.1 Individual Elements

The simplest way to examine and change a matrix element is to use the operator()(int,int) function, where the first argument gives the row, and the second argument gives the column. As with built-in C-style arrays, the first row or column is indexed with 0. For example, given a matrix A, the notation A(2,3) refers to row 2, column 3. Because numbering starts from 0, this is actually the third row and fourth column.

In the next example, the code prints the value of row 0, column 2, of the matrix A (A(0,2)), and then sets row 2, column 0 (A(2,0)) to 6:

cout << A(0,2) << endl;
A(2,0) = 6;

This code compiles correctly for any type of matrix A, and generally behaves correctly. However, there are two situations in which a runtime error could occur. These are discussed in the next two sections.

3.5.2 Bounds Checking

Bounds checking is done using operator()() only if the preprocessor symbol RWBOUNDS_CHECK is defined when the matrix header file is read in. Usually, this is done via a compiler flag, but for examples here we use explicit preprocessor directives. In the following code, the symbol RWBOUNDS_CHECK is defined, so it causes a runtime error.

#define RWBOUNDS_CHECK             // Do bounds checking
#include <rw/ctrdgmat.h>

main()
{
    // Define a 3x3 tridiagonal matrix and try to access
    // element (3,2), which does not exist!
    DComplexTriDiagMat A(3, 3);
    DComplex el = A(3,2);          // Fails here!!!
}

On the other hand, the out-of-bounds reference in this code:

#undef RWBOUNDS_CHECK              // No bounds checking
#include <rw/ctrdgmat.h>

main()
{
    // Define a 3x3 tridiagonal matrix and try to read
    // element (3,2), which does not really exist
    DComplexTriDiagMat A(3,3);
    DComplex el = A(3,2);          // No bounds check!!!
}

is undetected unless it causes a segmentation error. This is because bounds checking was not enabled. The results of examining an out-of-bounds element are undefined and likely to return garbage. The results of setting an out-of-bounds element are also undefined, but likely to bring disaster! It is an excellent idea to use bounds checking except when execution speed is very important.

3.5.3 Changing Elements with operator()()

The subscripting operator operator()(int,int) can be used to change elements in all matrix types. This can lead to runtime errors if you attempt to make changes that don't make sense. For example, consider the following program:

#include <rw/dtrdgmat.h>

main()
{
    DoubleTriDiagMat A(5, 5);
    A(4,0) = 7; // ERROR: Can't change this element
}

This program causes a runtime error because you can not change element (4, 0) of a tridiagonal matrix; it is defined to be 0.

Using operator()(int,int) to change elements can sometimes lead to side effects. For example, consider this program:

#include <rw/fskewmat.h>
#include <iostream.h>

main()
{
    FloatSkewMat A(2, 2);                           // 1
    A.zero();                                       // 2
    A(0,1) = 1;                                     // 3
    A(1,0) = 1;                                     // 4
    cout << A << endl;
}

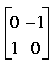
At first it looks like the output of this program should be a matrix with 0s on the diagonal and 1s in the other two entries. However, the actual output is:

The problem is that the matrix must be skew symmetric at all times; it is, after all, a skew symmetric matrix! Line //3 does indeed set the top right element to 1, but in order to retain the skew symmetric shape of the matrix, it also sets the bottom left element to -1. Line //4 then sets the bottom left element to 1, but also sets the top right element to -1 as a side effect. Thus //3 is irrelevant; it changes the same two elements as //4!

At this point, you may ask just how these checks and side effects are implemented. After all, operator()(int,int) can't know whether it is used as a left side or a right side. The answer is that for some matrix types, operator()(int,int) returns an instance of a helper class. This class has a function that converts it to the appropriate type if a right-side value is needed. It also has an operator=() function that is called if the class is used as an lvalue; the function sets a matrix element to a value. This provides enough indirection for everything we need to do. For general and symmetric matrix shapes, this indirection is not necessary and a regular C++ reference is returned. Details of the helper classes are given in Chapter 9 of this manual.

3.5.4 val() and set()

Generally, you can use the familiar subscripting operator operator()(int,int) to access or set any element. The syntax is natural and intuitive. However, using this simple approach may not always be optimal since, as we've seen, some matrix types require the use of a helper class for subscripting. This is because the subscripting operator can be used as either an lvalue or an rvalue and hence must work when both examining and setting an element. The use of this helper class may cause your code to be slightly larger and slower than necessary.

To avoid these problems, two additional member functions are provided for element access: val() and set(). Both of these are used in the following example:

#include <rw/chbndmat.h>               // Complex Hermitian banded

main()
{
    DComplexHermBandMat H(5,5,2);
    DComplex el = H.val(2,2);               // 1
    H.set(2,2,DComplex(3,2));               // 2
}

Let's consider each commented line:

//1

This line sets the complex variable el equal to the value of entry (2,2) of the matrix. As with the subscripting operator, bounds checking is done only if the preprocessor symbol BOUNDS_CHECK is defined when the header file is read. Using val() can generate smaller and faster code than the functionally equivalent line:

DComplex el = H(2,2);

because the subscripting operator for Hermitian matrices uses a helper class in order to maintain conjugate transpose symmetry within the matrix.

//2

This line sets entry (2,2) of the matrix equal to the complex number 3+2i. As before, bounds checking is done only if the preprocessor symbol BOUNDS_CHECK is defined when the header file is read. Also, as before, this can generate smaller and faster code than the equivalent:

H(2,2) = DComplex(3,2);

3.5.5 Rows, Columns and Diagonals

You can access entire rows and columns of general matrices, and diagonals of general, banded, and tridiagonal matrices, as easily as you can access individual elements. The functions rows(), cols(), and diagonal() return vectors corresponding to a row, column, or diagonal of the matrix. The resulting vector is a new view of the matrix's data and may be used as either a left side or a right side in expressions.

Just as with val() and set(), the functions rows(), cols() and diagonal() do bounds checking only if the preprocessor symbol RWBOUNDS_CHECK is defined when the header file is read. The function bcdiagonal() does the same thing as diagonal(), but does bounds checking regardless of whether or not RWBOUNDS_CHECK is defined when the header file is read.

3.5.6 Components of Complex Matrices

The real and imaginary parts of complex matrices are also easy to access. The member functions real() and imag() return a matrix containing the real or imaginary part. For example, consider the following code:

#include <rw/chermmat.h>
#include <rw/dsymmat.h>
#include <rw/dskewmat.h>

main()
{
    DComplexHermMat H(5, 5);              // 1
    DoubleSymMat Hreal = real(H);         // 2
    DoubleSkewMat Himag = imag(H);        // 3
}

//1	In `//1` the matrix `H` is defined to be a 5 x 5 Hermitian matrix. A Hermitian matrix is equal to its complex conjugate transpose; this implies that its real part is symmetric, and its imaginary part is skew symmetric.
//2	Here we extract the real part of `H`. Note that the global function `real()` is an overloaded function. The compiler selects the function with prototype: `DoubleSymMat real(const DComplexHermMat&);` Note that this function returns a symmetric matrix.
//3	Now the imaginary part of `H` is extracted. The function `imag()` has prototype: `DoubleSkewMat imag(const DComplexHermMat&);` and returns a skew symmetric matrix, just as the mathematics implies it must.

In this example, the matrices Hreal and Himag actually refer to the data of H; that is, they present different views of the same data as H. You can use this fact to conveniently modify the real and imaginary parts of a complex matrix in the following example:

#include <rw/cgenmat.h>
#include <rw/dgenmat.h>

main()
{
    RWGenMat<DComplex> A(5,5, rwUninitialized);              // 1
    real(A) = 1;                                             // 2
    imag(A) = -1;                                            // 3
}

//1	This line defines a 5 x 5 general complex matrix with double precision.
//2	The real parts of the matrix are set to 1.
//3	The imaginary parts of the matrix are set to -1.

3.5.7 Direct Access to Data

Advanced users may need to access the data stored in a matrix directly. This is especially important if you plan to interface a matrix type with another language, such as C or Fortran. The datavec() member function is provided for this purpose in all matrices except general matrices. To access the data in a general matrix, see the Math.h++ documentation. The rest of this section describes matrix types other than general matrices.

The data in a matrix is stored using the vector classes of Math.h++. The storage pattern for each matrix shape is described in detail in the Math.h++ Class Reference. The member function datavec() returns the vector holding the data. The following simple program illustrates how the data is arranged in a tridiagonal matrix:

#include <iostream.h>
#include <rw/dtrdgmat.h>

main()
{
    DoubleTriDiagMat A(4,4);                               // 1
    RWMathVec<double> Adata = A.dataVec();                 // 2
    Adata = RWMathVec<double>(Adata.length(),1,1);         // 3
    cout << A << endl;                                     // 4
}

Here is a description of what this program does:

//1	This line declares `A` to be a 4 x 4 tridiagonal matrix.
//2	This line accesses the data vector used to store the entries of `A`. This gives you a vector that references the same data as `A`.
//3	This line sets the data vector equal to a vector of the same length containing the elements 1,2,3,...
//4	This line prints the matrix. The entries are numbered according to their ordering in the data vector.

This program can be used to show you how the data is stored for any matrix type.

Sometimes it is useful to operate only on elements of a matrix that you know are explicitly stored. For example, you may want to set all elements of a banded matrix within the nonzero band equal to 1. The following shows how you could do this:

#include <rw/fbandmat.h>

main()
{
    FloatBandMat A(8,8,2,1);        // 1
    // A = 1 illegal                // 2
    A.dataVec() = 1;                // 3
}

Line //1 defines A to be an 8 x 8 banded matrix with an upper bandwidth of 2 and a lower bandwidth of 1. Line //2 in the program would not be legal; there is no operator=(float) function defined for a FloatBandMat. This is because setting the matrix equal to 1 would imply that every element in the matrix be set equal to 1. This is impossible because, for the matrix to remain banded, some of the entries are defined to be 0. Line //3 shows how to set all entries in the nonzero band to 1. The dataVec() function returns a reference to the vector used to store the nonzero elements. By setting this vector to 1, you can set all nonzero elements to 1.