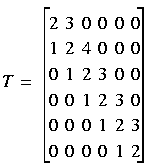3.2 Defining Matrices

Once we understand vectors, the next most important abstraction in linear algebra is the concept of a linear mapping from one vector space to another. Since we are concerned only with vectors of finite dimension, such a mapping can always be represented using a matrix of coefficients. If x is a vector from one space, and y is a vector from another, we can represent a linear mapping from x to y as y=Ax, where A is a matrix, and Ax is an inner product. Often, the matrix A has some special structure; for example, it may be banded or symmetric.

LAPACK.h++ has classes for many different matrix types. Each matrix type has a similar interface, so if you learn one, learning the others is easy. To give you a feel for using a matrix type, here is a simple example using a tridiagonal matrix class:

#include <rw/ftrdgmat.h>                          // 1
#include <iostream.h>

main()
{ 
    FloatTriDiagMat T(6,6);                       // 2
    T.zero();
    T.diagonal(0) = 2;                            // 3
    T.diagonal(-1) = 1;
    T.diagonal(1) = 3;
    T(1,2) = 4;                                   // 4
    RWMathVec<float> x = " [ 2 3 9 8 3 0 ] ";
    RWMathVec<float> Tx = product(T,x);           // 5
    cout << T << endl;
    cout << x << endl;
    cout << Tx << endl;
}

//1	The first line declares the class *FloatTriDiagMat* as a new C++ type by including the Rogue Wave header file `ftrdgmat.h`. A variable of type *FloatTriDiagMat* represents a tridiagonal matrix of floating point numbers. A tridiagonal matrix is a matrix where all the entries are 0, except for the entries on the main diagonal, and the entries immediately above and below the main diagonal.
//2	This line defines `T` to be an uninitialized 6 x 6 tridiagonal matrix; the next line sets all of its entries to 0.
//3	Here we use the diagonal function to set the entire main diagonal to 2. The next two lines set the other two nonzero diagonals to 1 and 3.
//4	In this line, we use subscripting to access a particular element of the matrix and change it. The matrix is set up as follows:

//5

Here Tx is defined to be the matrix-vector inner product of T and x. It may seem confusing at first not to use the function operator* to do matrix-vector multiplication, but there is a good reason for doing things this way. The overloaded operators +, -, *, and / are all used to do element-by-element operations; this symmetry in the operators make it easier to remember the effects of the operators.