5.4 Regression Analysis Classes

The Analytics.h++ library provides classes for performing analyses of overall model significance for linear and logistic regressions. These classes are RWLinearRegressionANOVA, RWLogisticFitAnalysis, and RWLinearRegressionFTest. Let's discuss these in more detail in the following sections.

5.4.1 Class RWLinearRegressionANOVA

Class RWLinearRegressionANOVA may be used to conduct an analysis of variance for a linear regression. The quantities calculated include: overall F statistic, residual sum of squares, regression sum of squares, degrees of freedom for the regression and residuals, mean square error, coefficient of determination, and adjusted coefficient of determination.

Using the class is fairly easy. You simply specify a linear regression object, either at construction time or via the member function setLinearRegression(), and query the object for the various ANOVA quantities. Here is a simple example:

  RWGenMat<double> predictorMatrix;    // Values for the predictor
                                       // variables
  RWMathVec<double> observationVector; // Values for the dependent
                                       // variable
 .
 .
 .
  RWLinearRegression lr( predictorMatrix, observationVector );
  if ( lr.fail() )     // Make sure the parameters were calculated
  {
    cerr << "linear regression calculation failed" << endl;
  }
  else
  {
    // Construct an ANOVA object from the linear regression model 
    // and print the results.
    RWLinearRegressionANOVA lrANOVA( lr );
    cout << "F statistic:  " << lrANOVA.FStatistic() << endl;
    cout << "F statistic p-value:  " << lrANOVA.FStatisticPValue()
             << endl;
    cout << "F statistic critical value:  " 
         << lrANOVA.FStatisticCriticalValue(.05) << endl;
    cout << "mean square residual  " 
         << lrANOVA.meanSquareResidual() << endl;
    cout << "mean square regression   " 
         << lrANOVA.meanSquareRegression() << endl;
    cout << "Rsquare:  " << lrANOVA.RSquare() << endl;
    cout << "adjusted Rsquare: " << lrANOVA.adjRSquare() 
         << '\n' << endl;
  }
  .
  .
  .

5.4.2 Class RWLogisticFitAnalysis

Class RWLogisticFitAnalysis is similar to class RWLinearRegression, which was described above. To use RWLogisticFitAnalysis, you specify a logistic regression, either at construction time or via the setLogisticRegression() member function, and query the object for the various fit analysis quantities. The following example demonstrates the procedure.

RWLogisticRegression model;
.
.
.
RWLogisticFitAnalysis logfit(model);

cout << "Pearson statistic: " << logfit.PearsonStatistic() << endl;
cout << "Pearson statistic p-value: " <<
            logfit.PearsonStatisticPValue() << endl;
cout << "Pearson statistic 10% critical value: " <<
            logfit.PearsonStatisticCriticalValue(0.10) << endl;
cout << "Pearson statistic degrees of freedom: " << 
            logfit.PearsonStatisticDegreesOfFreedom() << endl;
cout << "Predictor data groups for Pearson statistic: " <<
            logfit.predictorDataGroups() << endl;
cout << endl;

cout << "HL statistic: " << logfit.HLStatistic() << endl;
cout << "HL statistic p-value: " << logfit.HLStatisticPValue() <<
            endl;
cout << "HL statistic 10% critical value: " <<
            logfit.HLStatisticCriticalValue(0.10) << endl;
cout << "HL statistic degrees of freedom: " <<
            logfit.HLStatisticDegreesOfFreedom() << endl;
cout << "Bin counts for predictions: " <<
            logfit.HLStatisticOutputHistogram() << endl;
cout << "Bin counts for predictions associated \n
           with positive observations: " 
           << logfit.HLStatisticPosObsHistogram() << endl;
cout << endl;
.
.
.

5.4.3 Class RWLinearRegressionFTest

Suppose that we have the linear regression model:

and we want to test the hypothesis and the hypothesis .

We can express each of these hypotheses in the matrix form , where

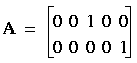, , for , and

for .

The RWLinearRegressionFTest class can be used for testing hypotheses of the above form , where is the vector of parameters for the linear regression model, is a known matrix of rank , and is a known vector. The following is an example that tests both types of hypotheses.

int main()
{
  RWGenMat<double> predictorMatrix;    // Predictor variable values
  RWMathVec<double> observationVector; // Dependent variable values
  double significanceLevel = .05;

  if ( !getDataFromFile("crime.dat", predictorMatrix,
                        observationVector) )
  {
    return 0;
  }

  RWLinearRegression lr( predictorMatrix, observationVector );
  RWLinearRegressionFTest FTest( lr );

  // Test that B3 = B4.
  RWGenMat<double> A( 1, lr.numParameters(), 0.0 );
  RWMathVec<double> c( 1, 0.0 );
  A(0,3) = 1.0;
  A(0,4) = -1.0;

  FTest.setHypothesis( A, c );

  cout << "F Test for H0 B3 = B4\n" << endl;
  cout << "  F statistic value:   " << FTest.FStatisticValue() <<
            endl;
  cout << "  F statistic p-value: " << FTest.FStatisticPValue() <<
            endl;
  cout << "  Critical value:      " <<
            FTest.criticalValue(significanceLevel) << '\n' << endl;
  if ( FTest.reject(significanceLevel) )
  {
    cout << "Reject H0 at significance level " << significanceLevel
            << endl;
  }
  else
  {
    cout << "Fail to reject H0 at significance level " <<
            significanceLevel << endl;
  }

  return 0;
}