Understanding the behavior of model selection tools is easiest when the model selection techniques are viewed as search techniques. The search space consists of possible subsets of predictor variables. An evaluation criterion assigns each subset a numerical value, and the goal of the search is to find the subset with the highest numerical value. The only difference between techniques involves the choice of a starting subset and the specification of neighboring subsets in the search space.
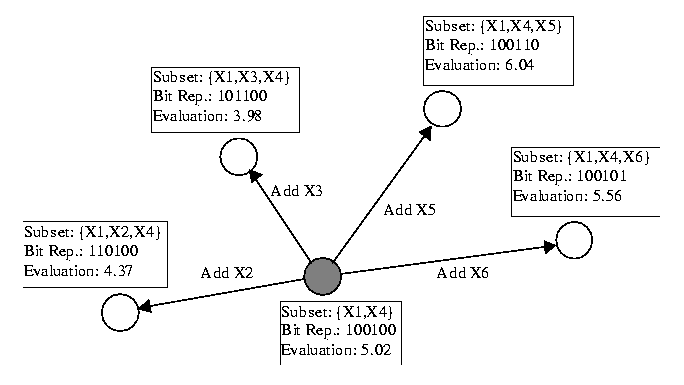
As an example, Figure 4 illustrates one model selection technique, forward selection, using a connected graph. In this particular example, there are six possible predictor variables:
. Nodes in the graph indicate predictor variable subsets; each node is labeled with the subset, a bit representation of the subset, and the subset's evaluation criterion. The current node in the search is shaded, while its neighboring nodes are not shaded. Graph edges indicate which subsets are considered neighbors in the search; edges are labeled with the action that changes the current subset into its neighbor. Search continues along the path in the graph that leads to the greatest evaluation criterion, and stops when the evaluation criterion can no longer improve. In the graph in Figure 4, forward selection adds the predictor variable
because the resulting predictor variable subset has the highest evaluation criterion with a value of 6.04. Then forward selection makes this subset the current one and continues by evaluating the new subset's neighbors. The new neighbors are not shown in the figure.
In general, exhaustive search is the only technique guaranteed to find the predictor variable subset with the best evaluation criterion. It is often the ideal technique when the number of possible predictor variables is less than 20; note that this number depends to some degree on the computational complexity of evaluating a predictor variable subset.
The problem with exhaustive search is that it is often a computationally intractable technique for more than 20 possible predictor variables. As Figure 4 shows, every possible subset of N predictor variables has a unique bit representation that uses N bits. It is easy to see that there are
possible subsets, excluding the empty set, and exhaustive search must check them all. For regression models with 25 predictor variables, exhaustive search must check 33,554,431 subsets, and this number doubles for each additional predictor variable considered. Clearly, exhaustive search is not always a practical technique, and other selection techniques may have to be considered.
Unlike exhaustive search, forward selection is always computationally tractable. Even in the worst case, it checks a much smaller number of subsets before finishing. This technique adds predictor variables and never deletes them. The starting subset in forward selection is the empty set. For a regression model with
possible predictor variables, the first step involves evaluating
predictor variable subsets, each consisting of a single predictor variable, and selecting the one with the highest evaluation criterion. The next step selects from among
subsets, the next step from
subsets, and so on. Even if all predictor variables are selected, at most
subsets are evaluated before the search ends.
The problem with forward selection is that, unlike exhaustive search, it is not guaranteed to find the subset with the highest evaluation criterion. In practice, however, many researchers have reported good results with forward selection (Miller, 1990).1 This is not too surprising: it's not hard to show that forward selection will find the subset with the highest evaluation criterion when predictor variables are statistically independent and the observation variable is modeled as a linear combination of predictor variables.2 While statistical independence of predictor variables may be too much to expect for the regression problem you are trying to improve, it may become more feasible with more study into the predictor variables. You may discover certain preprocessing steps that can be performed to predictor variable data such that the predictor variables become nearly statistically independent.
Backward selection has computational properties that are similar to forward selection. The starting subset in backward selection includes all possible predictor variables. Predictor variables are deleted one at a time as long as this results in a subset with a higher evaluation criterion. Again, in the worst case, at most
subsets must be evaluated before the search ends. Like forward selection, backward selection is not guaranteed to find the subset with the highest evaluation criterion.
Some researchers prefer backward selection to forward selection when the predictor variables are far from statistically independent. In this case, starting the search with all predictor variables included allows the model to take predictor variable interactions into account. Forward selection will not add two predictor variables that together can explain the variations in the observation variable if, individually, the predictor variables are not helpful in explaining the variation. Backward selection, on the other hand, would already include both of these variables and would realize that it is a bad idea to delete either one.
The disadvantage of backward selection is that one's confidence in subset evaluation criterion values tends to be lower than with forward selection. This is especially true when the number of rows in the predictor matrix is close to the number of possible predictor variables. In such a case, there are very few points that the regression model can use in order to determine its parameter values, and the function evaluation criterion will be sensitive to small changes to the predictor matrix data. When the ratio of predictor matrix rows to predictor variables is small, it is usually a better idea to use forward selection than backward selection.
Stepwise selection has been proposed as a technique that combines advantages of forward and backward selection. At any point in the search, a single predictor variable may be added or deleted. Commonly, the starting subset is the empty set. When we think in terms of a predictor variable subset's bit representation, stepwise selection allows one bit in the representation to be flipped at any point in the search. Therefore, since a subset's bit representation has
bits, each subset in the search graph for stepwise selection has
neighbors. If no bit is flipped more than once, at most
subsets are evaluated before stepwise selection ends. There are, however, no guarantees that each bit will be flipped at most one time.
No strong theoretical results exist for comparing the effectiveness of stepwise selection against forward or backward selection. Stepwise selection evaluates more subsets than the other two techniques, so in practice it tends to produce better subsets (Miller, 1990).3 Of course, the price that stepwise selection pays for finding better subsets is reduced computational speed: usually more subsets must be evaluated before the search ends.
©Copyright 1999, Rogue Wave Software, Inc.
Contact Rogue Wave about documentation or support issues.