Signals and Systems Used in Signal Processing
In mathematical terms, signals are functions of an independent variable, which may be continuous or discrete. By convention, the independent variable is referred to as “time.” Continuous-time signals are termed analog signals, while discrete-time signals are called digital. Discrete-time signals, also called sequences, are typically obtained by sampling continuous-time signals.
The PV‑WAVE Signal Processing Toolkit functions are used to process discrete-time or digital signals. Within the Signal Processing Toolkit, discrete-time signals are represented as arrays of numerical values that have been sequentially sampled at specific time intervals. In this manual, signals are referred to using the sequence notation:
x(n), n = 0, ..., N – 1
the same notation for accessing the elements of an array in PV-WAVE Advantage.
“Signal processing” refers to applying a function:
T(.)
to a signal x(n) to obtain a “processed” signal, y(n) = T(x(n)). The function
T(.)
is referred to as the system transfer function. The Signal Processing Toolkit provides a large class of routines that design and apply the transfer functions used most often in digital signal processing.
System Transfer Models and Digital Filter Data Structure
The definition of a system transfer function is very broad. By far, the most commonly used transfer functions are those that are linear and time-invariant.
Linear System Models
Linear and time-invariant systems are represented by the convolution operation:
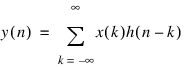
where the sequence h(n) is the impulse response of the system, x(k) is the signal input to the system, and y(n) is the response of the system. The class of linear time-invariant systems is very large. Among all such systems, the one defined by the linear constant-coefficient difference equation (EQ1) is central to practical applications of signal processing.
y(n) = b0x(n) + b1x(n – 1) + ... + bMx(n – M)
– a1y(n – 1) – a2y(n – 2) – ... – aNy(n – N) (EQ 1)
– a1y(n – 1) – a2y(n – 2) – ... – aNy(n – N) (EQ 1)
The z-transform of this difference equation is given by:
Y(z) = H(z)X(z)
where X(z) and Y(z) are the z-transforms of the sequences x(n) and y(n), respectively, and H(z) is the rational transfer function:
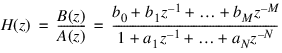(EQ 2) The function H(z) is simply referred to as a digital filter. If the filter coefficients satisfy an = 0 for n = 1, 2, ..., N, then the filter has finite impulse response (FIR). Otherwise, if an ≠ 0 for n > 1, the filter has infinite impulse response (IIR).
There are many ways to rearrange the difference equation (EQ 1) and transfer function (EQ 2). Standard canonic forms, in addition to the transfer function form (EQ 2), include the zero-pole-gain (first order cascade) form, second order cascade form, partial fraction (first order parallel) form, second order parallel form, and state-space form (for single input and single output). All of these canonic forms are theoretically equivalent to the transfer function form (EQ 2).
With finite precision arithmetic, the various canonic forms provide varying degrees of numerical precision. The PV‑WAVE Signal Processing Toolkit uses the transfer function canonic form, and all computations that use this canonic form are carried out using double-precision arithmetic. If you require any of the other canonic forms for their application, it is possible to transfer back and forth between the various forms using the fundamental polynomial manipulation functions (see "Polynomial Manipulation") provided in the Signal Processing Toolkit
Filter Data Structures
Because the rational transfer function model:
is so important to classical signal processing, the PV‑WAVE Signal Processing Toolkit uses a data structure to represent the rational transfer functions and simplify your task of keeping track of the numerator and denominator coefficients.
Routines for accessing the filter structure information are summarized in the following table. For detailed information, see Chapter 2: Reference (A to F) and Chapter 3: Reference (G to P).
Routine | Description |
|---|---|
FILTSTR (*) | Place information into filter structure. |
PARSEFILT (*) | Extract information from filter structure. |
* function uses the digital filter data structure | |
The basic information contained within the filter structure includes an array of real numerator coefficients, an array of real denominator coefficients, and a name string. Within the filter structure, the coefficients are represented in double precision.
All filter approximation and realization functions in the PV‑WAVE Signal Processing Toolkit use filter structures. The following example illustrates the use of a filter structure.
@sigpro_startup
; Numerator coefficients of the rational transfer function.
numerator = [1, 3, 3, 1]
; Denominator coefficients of the rational transfer function.
denominator = [1, 0, 1/3.0]
; Places the filter coefficients into the filter structure.
h = FILTSTR(numerator, denominator, Name = 'example')
; Extracts the filter coefficients from the filter structure.
PARSEFILT, h, filtname, b, a
PRINT, filtname
; PV-WAVE prints the following:
; example
PM, b
; PV-WAVE prints the following:
; 1.0000000
; 3.0000000
; 3.0000000
; 1.0000000
PM, a
; PV-WAVE prints the following:
; 1.0000000
; 0.0000000
; 0.3333333
Digital Filter Analysis Techniques
Two of the most basic techniques used in analyzing digital filters are determining the frequency response and determining the impulse response of a rational transfer function. The Signal Processing Toolkit functions that perform these operations are summarized in the following table. For detailed information, see Chapter 2: Reference (A to F) and Chapter 3: Reference (G to P).
Function | Description |
|---|---|
ABS * | Magnitude of each element in a complex array |
ARG | Phase angle of each element in a complex array |
FREQRESP_S ** | Complex frequency response of analog transfer function (Bode plot) |
FREQRESP_Z ** | Complex frequency response of digital transfer function |
IMPRESP | Impulse response of a filter |
* function reference found in PV-WAVE Reference ** function uses the digital filter data structure | |
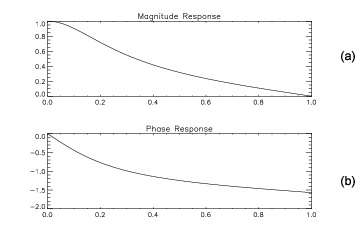
The following example illustrates the use of the filter analysis functions by computing the frequency response of a first order Butterworth lowpass filter with a normalized frequency cutoff of 0.2049. The resulting magnitude and phase plots for the frequency response of the filter in this example code are shown in Figure 1-1: Magnitude (a) and Phase (b) Response of First-Order Butterworth Filter.
; Places Butterworth filter coefficients into filter structure.
h = FILTSTR([.25, .25],[1, -.5])
; Computes the complex frequency response of the filter on the
; unit circle.
hf = FREQRESP_Z(h, Outfreq = f)
; Produce one column of two plots.
!P.Multi = [0, 1, 2]
; Plot the magnitude of the complex frequency response.
PLOT, f, ABS(hf), Title = 'Magnitude Response'
; Plot the phase of the complex frequency response.
PLOT, f, ARG(hf), Title = 'Phase Response'
 |
