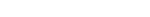CSINTERP Function
Computes a cubic spline interpolant, specifying various endpoint conditions. The default interpolant satisfies the not-a-knot condition.
Includes keywords to compute a tension-continuity-bias (TCB) cubic spline interpolant.
Usage
result = CSINTERP(xdata, fdata)
Input Parameters
xdata—One-dimensional array containing the abscissas of the interpolation problem.
fdata—One-dimensional array containing the ordinates for the interpolation problem.
Returned Value
result—A structure that represents the cubic spline interpolant.
Input Keywords
Double—If present and nonzero, double precision is used.
ILeft—Sets the value for the first or second derivative of the interpolant at the left endpoint. Keyword ILeft is used to specify which derivative is set: ILeft = 1 for the first derivative and ILeft = 2 for the second derivative. The only valid values for ILeft are 1 or 2. If ILeft is specified, then Left also must be used.
Left—Sets the value for the first or second derivative of the interpolant at the left endpoint. If ILeft = i, then the interpolant s satisfies s(i)(xL) = Left. Here, xL is the leftmost abscissa.
IRight—Sets the value for the first or second derivative of the interpolant at the right endpoint. Keyword IRight is used to specify which derivative is set: IRight = 1 for the first derivative and IRight = 2 for the second derivative. The only valid values for IRight are 1 or 2. If IRight is specified, then Right also must be used.
Right—Sets the value for the first or second derivative of the interpolant at the right endpoint. If IRight = i, then the interpolant s satisfies s(i)(xR) = Right. Here, xR is the rightmost abscissa.
Periodic—If present and nonzero, computes the C2 periodic interpolant to the data. The following is satisfied:
s(i) (xL) = s(i) (xR) i = 0, 1, 2
where s, xL, and xR are defined above.
TCB Keywords
These keywords allow you to compute a tension-continuity-bias (TCB) cubic spline interpolant. This is also called a Kochanek-Bartels spline and is a generalization of the Catmull–Rom spline. To enable this functionality, you must enable the Tcb keyword.
Tension—Sets the tension values at the data points. The array Tension is of length ndata and contains tension values in the interval [–1,1], where ndata is the number of data points. For each point, if the tension value is near +1 the curve is tightened at that point. If it is near –1, the curve is slack. Default: All values of Tension are zero.
Continuity—Sets the continuity values at the data points. The array Continuity is of length ndata and contains continuity values in the interval [–1,1]. For each point, if the continuity value is zero the curve is C1 at that point. Otherwise the curve has a corner at that point, but is still continuous (C0). Default: All values of Continuity are zero.
Bias—Sets the bias values at the data points. The array Bias is of length ndata and contains bias values in the interval [–1,1]. For each point, if the bias value is zero the left and right side tangents are equally weighted. If the value is near +1 the left-side tangent dominates. If the value is near –1 the right-side tangent dominates. Default: All values of Bias are zero.
Tcb—If present and nonzero, this option turns on a tension-continuity-bias (TCB) cubic spline interpolant computation. By default, TCB computations are not enabled.
Discussion
Function CSINTERP computes a C2 cubic spline interpolant to a set of data points (xi, fi) for the following:
i = 0, ..., (N_ELEMENTS(xdata) – 1) = (n – 1)
The breakpoints of the spline are the abscissas. For all univariate interpolation functions, the abscissas need not be sorted. Endpoint conditions are to be selected by the user. The user can specify not-a-knot, or first or second derivatives at each endpoint or C2 periodicity can be requested (see de Boor 1978, Chapter 4). If no defaults are selected, then the not-a-knot spline interpolant is computed. If the Periodic keyword is selected, then all other keywords are ignored and a C2 is computed. In this case, if the fdata values at the left and right endpoints are not the same, a warning message is issued and the right value is set equal to the left. If Left and ILeft or Right and IRight are selected, the user has the ability to select the values of the first or second derivative at either endpoint. The default case (when the keyword is not used) is the not-a-knot condition on that endpoint. Thus, when no keywords are chosen, this function produces the not-a-knot interpolant.
If the data (including the endpoint conditions) arise from the values of a smooth (for example, C4) function f, i.e., fi = f(xi), then the error behaves in a predictable fashion. Let ξ be the breakpoint vector for the above spline interpolant. Then, the maximum absolute error satisfies:
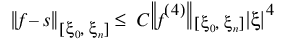
where the following is true:
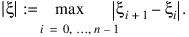
Example 1
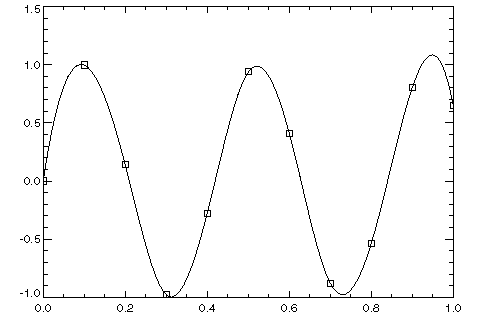
In this example, a cubic spline interpolant, as shown in Figure 4-1: Cubic Spline Interpolant, to function values is computed and plotted along with the original data. Since the default settings are used, the interpolant is determined by the not-a-knot condition (see de Boor 1978).
; Generate the abscissas.
x = FINDGEN(11)/10
; Generate the function values.
f = SIN(15 * x)
; Compute the spline interpolant.
pp = CSINTERP(x, f)
ppval = SPVALUE(FINDGEN(100)/99, pp)
; Plot the results.
PLOT, FINDGEN(100)/99, ppval
OPLOT, x, f, Psym = 6
 |
Example 2
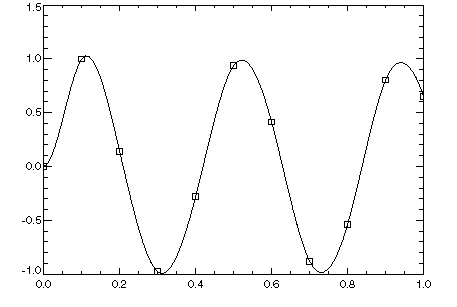
In this example, a cubic spline interpolant to function values is computed. The value of the derivative at the left endpoint and the value of the second derivative at the right endpoint are specified. The resulting spline and original data are then plotted as shown in Figure 4-2: Cubic Spline Interpolant with Endpoint Conditions.
x = FINDGEN(11)/10
y = SIN(15 * x)
pp = CSINTERP(x, y, ILeft = 1, Left = 0, $
IRight = 2, Right = -225 * SIN(15))
ppval = SPVALUE(FINDGEN(100)/99, pp)
PLOT, FINDGEN(100)/99, ppval
OPLOT, x, y, Psym = 6
 |
Warning Errors
MATH_NOT_PERIODIC—Data are not periodic. The rightmost fdata value is set to the leftmost fdata value.
Fatal Errors
MATH_DUPLICATE_XDATA_VALUES—The xdata values must be distinct.