POLY_2D Function
Performs polynomial warping of images.
Usage
result = POLY_2D(array, coeffx, coeffy[, interp[, dimx, ..., dimy]])
Input Parameters
array — The array to be processed. Must be two-dimensional. Can be of any basic type except string.
coeffx — The x coefficients.
coeffy — The y coefficients.
interp — (optional) If present and nonzero, specifies that the bilinear interpolation method is to be used in the resampling. Otherwise, the nearest neighbor method is used.
dimx — (optional) If present, specifies the number of columns in the resulting array. Otherwise, the output has the same number of columns as array.
dimy — (optional) If present, specifies the number of rows in the resulting array. Otherwise, the output has the same number of rows as array.
Returned Value
result — A two-dimensional array containing the warped image. It is of the same data type as array.
Keywords
Missing — Specifies the output value for points whose x', y' is outside the bounds of array. (If this keyword is not used, these values are extrapolated from the nearest pixel of array.)
Discussion
POLY_2D performs a geometrical transformation in which the resulting array is defined by:
g(x,y) = f(x', y') = f [a(x,y), b(x,y)]
where g(x,y) represents the pixel in the output image at coordinate (x, y), and f(x', y') is the pixel at (x', y') in the input image that is used to derive g(x, y).
The functions a(x, y) and b(x, y) are polynomials in x and y of degree n, and specify the spatial transformation:
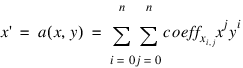
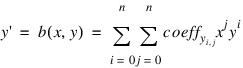
where n is the degree of the polynomials that are being used to produce the warping, and coeffx and coeffy are arrays containing the polynomial coefficient. Each array must contain (n + 1)2 elements.
For example, for a linear transformation, coeffx and coeffy must contain four elements and may be either a 2-by-2 array or a 4-element vector. Cxi,j contains the coefficient used to determine x', and is the weight of the term xjyi.
The nearest neighbor interpolation method is not linear, because new values that are needed are merely set equal to the nearest existing value of image. For more information on bilinear interpolation, see the BILINEAR function.
Bilinear interpolation can be time-consuming. For example, it requires about twice as much time as does the nearest neighbor method, even if you are working with a linear case (in other words, if n equals 1).
|
Note: |
The POLYWARP function may be used to fit (x', y') as a function of (x, y) and return the coefficient arrays Cx and Cy. |
The POLY_2D function supports multi-layer band interleaved images. When the input array is three-dimensional, it is automatically treated as an array of images, array(m, n, p), where p is the number of m by n images. Each image is then operated on separately and an array of the result images is returned.
Example
Some simple linear (degree one) transformations are shown in Linear Transformations.
|
P0,0 |
P1,0 |
P0,1 |
P1,1 |
Q0,0 |
Q1,0 |
Q0,1 |
Q1,1 |
Effect |
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
Identity |
|
0 |
0 |
0.5 |
0 |
0 |
1 |
0 |
0 |
Stretch x by a factor of 2 |
|
0 |
0 |
1 |
0 |
0 |
2.0 |
0 |
0 |
Shrink y by a factor of 2 |
|
z |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Shift left by z pixels |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
Transpose |
See Also
BILINEAR, POLY, POLY_FIT, POLYWARP
For details on interpolation methods. see the section Efficiency and Accuracy of Interpolation in Chapter 6 of the PV‑WAVE User Guide.





