Implements the morphologic erosion operator for shape processing.

image—The array to be eroded.

structure—The structuring element. May be a one- or two-dimensional array. Elements are interpreted as binary (values are either zero or nonzero), unless the Gray keyword is used.

x0—(optional) The x-coordinates of structure’s origin.

y0—(optional) The y-coordinates of structure’s origin.

result—The eroded image.

Gray—A flag which, if present, indicates that gray scale, rather than binary erosion, is to be used.

Values—An array providing the values of the structuring element. Must have the same dimensions and number of elements as structure.

If image is not of the byte type, PV-WAVE makes a temporary byte copy of image before using it for the processing.

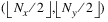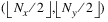The optional parameters x0 and y0 specify the row and column coordinates of the structuring element’s origin. If omitted, the origin is set to the center, , where Nx and Ny are the dimensions of the structuring element array. However, the origin need not be within the structuring element.

Nonzero elements of the structure parameter determine the shape of the structuring element (neighborhood).

If the Values keyword is not used, all elements of the structuring element are 0, yielding the neighborhood minimum operator.

You can choose whether you want to use gray scale or binary erosion:

The ERODE function implements the morphologic erosion operator on binary and gray scale images and vectors. Mathematical morphology provides an approach to the processing of digital images on the basis of shape. This approach is summarized in the description of the DILATE function. Erosion is the complement (dual) of dilation; it does to the background what dilation does to the foreground.

Briefly, ERODE returns the erosion of image by the structuring element, structure. This operation is also commonly known as contracting or reducing. It can be used to remove islands smaller than the structuring element.

The result is an image that contains items that now contract away from each other. Features that either slightly touch or are connected by narrow areas may disconnect, becoming separate, smaller objects. Any holes or gaps in or between features become larger as the features in the image shrink away from each other. Sharp-edged items and harsh angles typically become dull as they are worn away; however, in some cases areas that were dull may become somewhat sharper as a feature erodes away.

Used with gray scale images, which are always converted to a byte type, the ERODE function is accomplished by taking the minimum of a set of differences. It may be conveniently used to implement the neighborhood minimum operator, with the shape of the neighborhood given by the structuring element.

Used with binary images, the origin of the structuring element is moved to each pixel of the image. If each nonzero element of the structuring element is contained in the image, the output pixel is set to one.

Letting A θ B represent the erosion of an image A by structuring element B, erosion may be defined as:

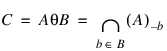
where (A)–b represents the translation of A by b. The structuring element B may be visualized as a probe which slides across the image A, testing the spatial nature of A at each point. Where B translated by i, j can be contained in A (by placing the origin of B at i, j), then Ai, j belongs to the erosion of A by B.

For example, when the origin of the structuring element is at (0, 0) it would look like:

This example demonstrates what an aerial image looks like before and after applying the ERODE function three different times. Figure 6-1: Using the ERODE Function shows the results. The image on the left is the “before” image and the image on the right is the “after” picture. For this example, the following parameters were used each time:

LOADCT, 0

OPENR, lun, !Dir + '/demo/gallery3/data/aerial_demo.img', /Get_lun

aerial_img = BYTARR(512,512)

READU, lun, aerial_img

FREE_LUN, lun

struct = [1, 0, 1]

eroded_img = ERODE(aerial_img, struct, /Gray)

eroded_img = ERODE(eroded_img, struct, /Gray)

eroded_img = ERODE(eroded_img, struct, /Gray)

eroded_img = BYTSCL(eroded_img, Min=104)

WINDOW, Xsize=1024, /Free

TVSCL, aerial_img, 2

TVSCL, eroded_img, 1

where struct has a value of [1 0 1].