Lesson 1: Creating and Customizing Maps
This section explains how to create maps in PV‑WAVE using the MAP procedure and its keywords. In addition, procedures for annotating maps, creating map overlays, and combining maps and images are discussed.
In this lesson, you’ll do the following:
Plotting a World Map
The MAP procedure, by default, displays a world coastline map taken from the World Databank II dataset.
In this example, keywords are used to specify the range of data, select the map features to plot, create longitude/latitude gridlines, and add color. MAP accepts some additional optional keywords. For a complete list and description of the keywords, see the description of MAP in the PV‑WAVE Reference.
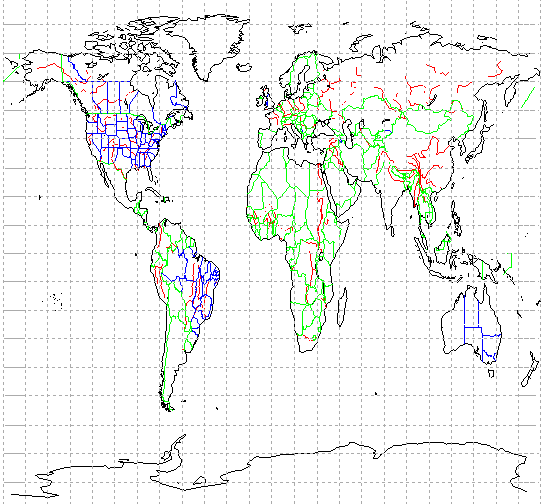
To produce the map shown in Figure 8-3: Equidistant Cylindrical Projection, do the following:
TEK_COLOR
MAP, Range=[-180, -90, 180, 90], $
Select={,GROUP:['cil','bdy','pby', 'riv']}, $
Color=-1, /Gridlines, Gridstyle=1, $
Gridcolor=WoColorConvert(15)
 |
Subsetting the Map Dataset
This section discusses the Select, Range, Zoom, Center, and Resolution keywords. These MAP keywords are used to subset the map dataset in different ways.
Selecting Map Attributes
Use the MAP Select keyword to specify the type(s) of map data (attributes) to plot.
To use the Select keyword, you need to know the special attributes (e.g., cities, political boundaries, rivers, continents) that are defined in the dataset. For example, the World Databank II includes coastlines, international boundaries, state boundaries, and rivers.
To use the Select keyword to specify that “CIL” (coastline, island, and lake) and “RIV” (river) data be plotted, do the following:
MAP, SELECT={, GROUP: ['CIL', 'RIV']}note | The Select keyword takes an unnamed structure as its input. For information on unnamed structures, refer to the PV‑WAVE Programmer’s Guide. |
Specifying the Map Limits
There are two ways to specify the portion of a map dataset to display. You can use the Range keyword or the Zoom and Center keywords.
Range Keyword
The Range keyword specifies the range of longitude and latitude values to be displayed. Range requires a four-element array containing the minimum longitude, minimum latitude, maximum longitude, and maximum latitude values to be plotted.
To use the Range keyword, you need to know the extent of the map data (its range in longitude and latitude). The World Databank II dataset, for example, is global in extent.
For example, the following MAP command uses the World Databank II data and plots the world map from between –90 and 90 degrees longitude and between –45 and 45 degrees latitude.
MAP, RANGE=[-90, -45, 90, 45]
Zoom and Center
For some applications the Zoom and Center keywords might be more convenient to use than the Range keyword to specify map limits.
To “zoom” in on a point on a map, use the Zoom and Center keywords. Center specifies a two-element array containing the longitude and latitude of the point to zoom in on. The Zoom keyword specifies a “zoom factor”. A zoom factor of 1 (the default) plots the entire globe. A zoom factor of 2 plots one-half of the globe, and so on.
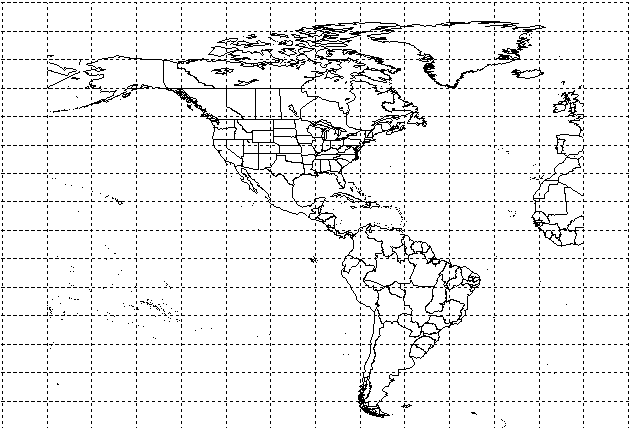
For example, the following MAP call produces the plot shown in Figure 8-4: Partial World Map Plotted with Center and Zoom Keywords.
MAP, Center=[-90, 30], Zoom=2, /Gridlines, Gridstyle=1
 |
Plotting Great Circles, Straight Lines, and Text
Use the MAP_PLOTS procedure to draw great circles or arbitrary straight lines on a map. MAP_PLOTS can also be used to compute geographical distances. To annotate a map, use the MAP_XYOUTS procedure.
A great circle is the intersection between a plane passing through the center of a sphere and the surface of a sphere. On a map, great circle lines represent the shortest distance between two geographical points. On most projections, great circles appear as curved lines.
By default, MAP_PLOTS computes the great circle between two points on a map projection and draws the great circle line.
Use MAP_PLOTS with the NoCircle keyword to draw straight lines between two points on a map. Straight lines can be used to highlight or draw attention to a particular feature. The lines drawn are not great circle lines.
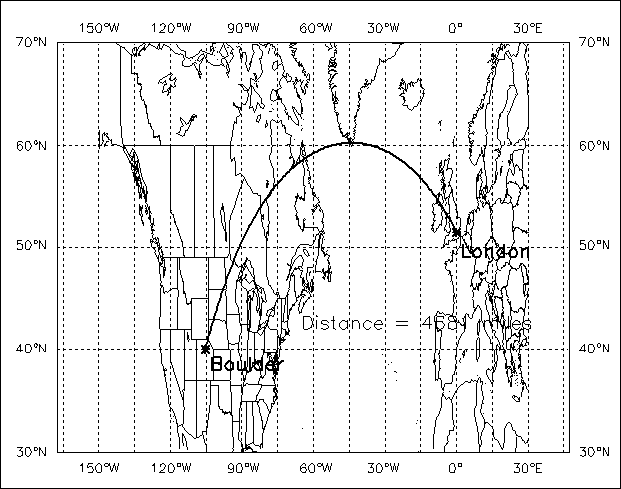
The following example uses MAP, MAP_PLOTS and MAP_XYOUTS to plot a great circle between two cities (Boulder, Colorado and London, England) and label the cities. The distance between the cities is also calculated and placed into a text label. (The map produced by this code is shown in Figure 8-5: Map Projection with Great Circle Arc.)
To plot a great circle from Boulder, CO to London, do the following:
1. Load a colortable.
TEK_COLOR
2. Plot the map. Enter the following at the WAVE> prompt:
MAP, RANGE=[-150, 30, 30, 70], /Axes, $
/GridLines, GridColor=WoColorConvert(10), GridStyle=1
3. Plot a great circle between two points. Return the distance between the points with the Distance keyword.
MAP_PLOTS, [-105.3, -0.1], [40.0, 51.5], Distance=d, $
/Miles, Color=WoColorConvert(5), Psym=-2, Thick=2
4. Label Boulder.
MAP_XYOUTS, -103.0, 38.0, 'Boulder', $
Color=WoColorConvert(5), Charsize=1.5, Charthick=2
5. Label London.
MAP_XYOUTS, 2.0, 49.0, 'London', $
Color=WoColorConvert(5), Charsize=1.5, Charthick=2
6. Add a text string containing the distance.
MAP_XYOUTS, -65.0, 42.0, $
'Distance ='+STRCOMPRESS(STRING(d(0), Format='(I5)')) $
+ ' miles', Color=WoColorConvert(5), Charsize=1.5
 |
Adding an Image Under the Map
Use the Image keyword to specify the name of an image (2D array) to be drawn under the map. The image is warped to fill the entire area specified by the Range keyword.
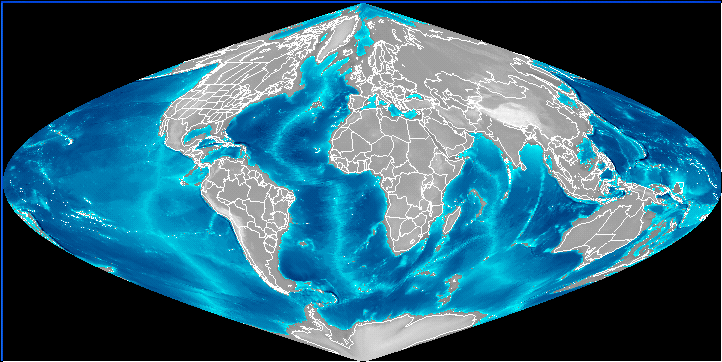
The following example warps a 2D array of global elevation data onto a sinusoidal map projection of the earth.
To create a sinusoidal map projection, do the following:
1. Get the path/filename of file containing a 2D array of global elevation data.
(WIN) file = GETENV("RW_DIR") + '\mapping-2_0\data\earth_elev.dat'
(UNIX) file = '$RW_DIR/mapping-2_0/data/' + $
'earth_elev.dat'
'earth_elev.dat'
2. Create array to hold image.
elev = FLTARR(720, 360)
3. Open and read the image data file into the array.
OPENR, 1, file, /Xdr
READU, 1, elev
CLOSE, 1
4. Open a window for displaying the plot.
WINDOW, Xsize=720, Ysize=360, Colors=128
5. Define and load a colortable.
TVLCT, 150, 150, 150, 63
red = BYTARR(127)
grn = BYTSCL(FINDGEN(127)^2.0)
blu = BYTSCL((FINDGEN(127)))
TVLCT, red, grn, blu, 0
TVLCT, 255, 255, 255, 127
6. Reference the image array with the Image keyword to warp the image around the map projection.
MAP, Projection=4, Range=[-180,-90,180,90], Image=elev
The map produced by this example is shown in Figure 8-6: Map Projection with Underlying Global Elevation Data.
 |
Adding Contour Lines
MAP_CONTOUR lets you overlay contours on a map. This routine works like the regular CONTOURFS procedure in PV‑WAVE, except that MAP_CONTOUR assumes that the X and Y vectors specified or created by default are specified in terms of longitude and latitude coordinates.
When plotted, the contour data is projected so that the contour lines accurately describe features on the surface of the globe.
To plot contour data on a map, do the following:
1. Get the path of file containing 2D array of global elevations.
(WIN) file = GETENV("RW_DIR") + '\mapping-2_0\data\earth_elev.dat'
(UNIX) file = '$RW_DIR/mapping-2_0/data/' + 'earth_elev.dat'
2. Create an array to hold the image.
elev = FLTARR(720, 360)
3. Open and read the image data file into the array.
OPENR, 1, file, /Xdr
READU, 1, elev
CLOSE, 1
water = BYTSCL(elev, Max=0.0, Top=63)
land = BYTSCL(elev, Min=0.0, Top=63)
elev = water + land
elev = REBIN(elev, 360, 180)
DATA = FLOAT(elev(-150+180:30+180, 30+90:70+90))
4. Subset the array of elevation data. The elevation dataset contains an elevation for each degree of longitude and latitude, from –180 to 180 degrees longitude and from –90 to 90 degrees latitude. The array expressions in this command subset the data corresponding to the range of data used in the MAP procedure call.
MAP, Projection=4, Range=[-150, 30, 30, 70], Thick=2
TEK_COLOR
MAP_CONTOUR, DATA, C_Colors=[2,8,16,18,20,4], $
Levels=[20,30,35,40,50]
The result is shown in Figure 8-7: Contour Lines over Map Projection.
 |
note | MAP_CONTOUR with the Fill keyword is not supported for projection 99 (Satellite), but good results can be obtained by creating a two-dimensional image with CONTOURFS and POLYCONTOUR and then using the Image keyword with MAP to wrap this image onto the globe. |
Adding Vector Lines
MAP_VELOVECT creates two-dimensional velocity vector plots. It works just like the PV‑WAVE VELOVECT procedure, except that MAP_VELOVECT takes longitude and latitude coordinates as input.
To add vector lines to a map, do the following:
1. Create two arrays.
u = FLTARR(20, 20)
v = FLTARR(20, 20)
2. Create the velocity vectors.
FOR j=0, 19 DO BEGIN $
FOR i=0, 19 DO BEGIN $
x = 0.05 * float(i) & $
z = 0.05 * float(j) & $
u(i,j) = -sin(!Pi*x) * cos(!Pi*z) & $
v(i,j) = cos(!Pi*x) * sin(!Pi*z)
3. Plot the velocity vectors on the map.
MAP, Projection=4, Range=[-150, 30, 30, 70]
MAP_VELOVECT, u, v, Color=5
When the vector lines are plotted, the current map projection is taken into account so that the vector lines are depicted accurately on the map, as shown in Figure 8-8: Vector Lines Added to Map Projection.
 |





