Image Sharpening
This section discusses some image sharpening methods. For more details on the functions described here, see the PV‑WAVE Reference.
The ROBERTS Function
An image may be sharpened (its edges or high spatial frequency components enhanced) by differentiation. One approximation to the derivative or gradient of the image is the Roberts Gradient, a form of cross difference, which is computed using the formula:
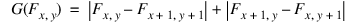
The ROBERTS function returns this result.
The SOBEL Function
Another commonly used gradient operator is the Sobel operator. It operates over a 3-by-3 region, making it less sensitive to noise than an operator with a smaller neighborhood. The SOBEL function returns an approximation to the Sobel operator:
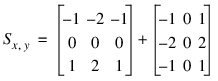
where the notation:

indicates the absolute value of the sum of the pixels in the 3-by-3 neighborhood surrounding the pixel at x, y, multiplied by the respective weights. The first term approximates the gradient in the y direction and the second term approximates the gradient in the x direction.
Unsharp Masking Method
Another method of sharpening images is unsharp masking. This method subtracts a smoothed image (which contains only low frequency components) from the original image, leaving an image containing only high frequency components. This process emphasizes the edges and small, sharp features. To unsharp mask and display an image using a 3-by-3 neighborhood, use the command:
TVSCL, A - SMOOTH(A,3)
The CONVOL Function
The same result can be obtained by convolving the image with the kernel:
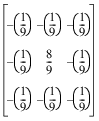
or:
TVSCL, CONVOL(A, [[–1,–1,–1],[–1,8,–1], [–1,–1,–1]],9)
The time required by the CONVOL function can become excessively long when the kernel or image is large. The time required is proportional to n2m2, where n is the size of the kernel and m is the size of the square image. Doubling the size of the kernel increases the time by a factor of four. The algorithm used in the SMOOTH function requires time in proportion to 2nm2, implying that it is almost always more efficient to use SMOOTH rather than CONVOL where possible.





