AUTO_UNI_AR Function
Automatic selection and fitting of a univariate autoregressive time series model. The lag for the model is automatically selected using Akaike’s information criterion (AIC). Estimates of the autoregressive parameters for the model with minimum AIC are calculated using method of moments, method of least squares, or maximum likelihood.
Usage
result = AUTO_UNI_AR(z, maxlag)
Input Parameters
z—Array containing the stationary time series.
maxlag—Maximum number of autoregressive parameters requested. It is required that 1 ≤ maxlag ≤ n_obs/2, where n_obs is the number of observations in the time series.
Returned Value
result—Array containing the estimates for the constant followed by the estimates for the autoregressive parameters in the model with minimum AIC.
Input Keywords
Double—If present and nonzero, double precision is used.
Maxit—Maximum number of estimation iterations. Default: Maxit = 300
Method—Estimation method option:
0—Method of moments1—Method of least squares realized through Householder transformations2—Maximum likelihoodDefault: Method = 1
Output Keywords
Avar—Estimate of innovation variance.
Aic—Minimum AIC.
Z_mean— (Input/Output) On input contains the estimate of the mean of the time series z. On output, Z_mean contains an update of the mean. Default: Time series z is centered about its sample mean.
Discussion
AUTO_UNI_AR automatically selects the order of the AR model that best fits the data and then computes the AR coefficients. The algorithm used in AUTO_UNI_AR is derived from the work of Akaike, H., et. al (1979) and Kitagawa and Akaike (1978). This code was adapted from the UNIMAR procedure published as part of the TIMSAC-78 Library.
The best fit AR model is determined by successively fitting AR models with 0, 1, 2, ..., maxlag autoregressive coefficients. For each model, Akaike’s Information Criterion (AIC) is calculated based on the formula:
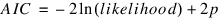
AUTO_UNI_AR uses the approximation to this formula developed by Ozaki and Oda (1979):
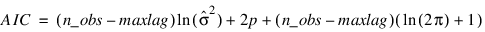
where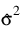 
is an estimate of the residual variance of the series, commonly known in time series analysis as the innovation variance.
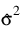is an estimate of the residual variance of the series, commonly known in time series analysis as the innovation variance.The best fit model is the model with minimum AIC. If the number of parameters in this model is equal to the highest order autoregressive model fitted, i.e., p = maxlag, then a model with smaller AIC might exist for larger values of maxlag. In this case, increasing maxlag to explore AR models with additional autoregressive parameters might be warranted.
If Method = 0, estimates of the autoregressive coefficients for the model with minimum AIC are calculated using method of moments. If method =1, the coefficients are determined by the method of least squares applied in the form described by Kitagawa and Akaike (1978). Otherwise, if Method = 2, the coefficients are estimated using maximum likelihood.
Example
Consider the Wolfer Sunspot data (Anderson 1971, p. 660) consisting of the number of sunspots observed each year from 1770 through 1869. In this example, AUTO_UNI_AR found the minimum AIC fit is an autoregressive model with 3 lags:
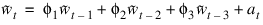
where:
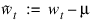
μ the sample mean of the time series {wt}. Defining the overall constant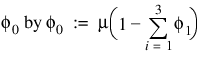 
, we obtain the following equivalent representation:
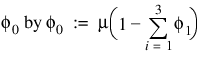, we obtain the following equivalent representation:
The example computes estimates for φ0, φ1, φ2, φ3, for each of the three parameter estimation methods available.
; Compute AR parameters for minimum AIC by method of moments
n_obs = 100 ; Total number of observations
maxlag = 20 ; Maximum number of autoregressive parameters
; requested
z = FLTARR(n_obs) ; The array containing the time series
w = STATDATA(2) ; Get wolfer sunspot data
FOR i=0L, n_obs-1 DO z(i) = w(21+i,1)
; Compute AR parameters for minimum AIC by method of moments
parameters = AUTO_UNI_AR(z, maxlag, $
Avar=avar, $
Method=0, $
Aic=aic)
p = N_ELEMENTS(parameters)
PRINT, "AIC Automatic Order selection"
PRINT, "AR coefficients estimated using method of moments"
PRINT, p-1, Format="('Order selected: ', I1)"PRINT, aic, avar, $
Format="('AIC = ', F10.4, ', Variance = ', F10.4)"PRINT, parameters(0), $
Format="('Constant estimate is ', F9.4)"PRINT, "Final AR coefficients estimated by method of moments"
PRINT, parameters(1:(p-1)), Format='(F10.3)'
PRINT, ''
; Compute AR parameters for minimum AIC by method of
; least squares.
parameters = AUTO_UNI_AR(z, maxlag, $
Avar=avar, $
Method=1, $
Aic=aic)
p = N_ELEMENTS(parameters)
PRINT, "AIC Automatic Order selection"
PRINT, "AR coefficients estimated using method of " + $
"least squares"
PRINT, p-1, Format="('Order selected: ', I1)"PRINT, aic, avar, $
Format="('AIC = ', F10.4, ', Variance = ', F10.4)"PRINT, parameters(0), $
Format="('Constant estimate is ', F9.4)"PRINT, "Final AR coefficients estimated by method of " + $
"least squares"
PRINT, parameters(1:(p-1)), Format='(F10.3)'
PRINT, ''
; Compute AR parameters for minimum AIC by maximum
; likelihood estimation
parameters = AUTO_UNI_AR(z, maxlag, $
Avar=avar, $
Method=2, $
Aic=aic)
p = N_ELEMENTS(parameters)
PRINT, "AIC Automatic Order selection"
PRINT, "AR coefficients estimated using method of " + $
"maxiumum likelihood"
PRINT, p-1, Format="('Order selected: ', I1)"PRINT, aic, avar, $
Format="('AIC = ', F10.4, ', Variance = ', F10.4)"PRINT, parameters(0), $
Format="('Constant estimate is ', F9.4)"PRINT, "Final AR coefficients estimated by method of "
PRINT, "maxiumum likelihood"
PRINT, parameters(1:(p-1)), Format='(F10.3)'
Output
AIC Automatic Order selection
AR coefficients estimated using method of moments
Order selected: 3
AIC = 554.0114, Variance = 287.2694
Constant estimate is 13.7098
Final AR coefficients estimated by method of moments
1.368
-0.738
0.078
AIC Automatic Order selection
AR coefficients estimated using method of least squares
Order selected: 3
AIC = 554.0114, Variance = 144.7149
Constant estimate is 9.8934
Final AR coefficients estimated by method of least squares
1.604
-1.024
0.209
AIC Automatic Order selection
AR coefficients estimated using method of maxiumum likelihood
Order selected: 3
AIC = 554.0114, Variance = 218.8337
Constant estimate is 11.3902
Final AR coefficients estimated by method of
maxiumum likelihood
1.553
-1.001
0.205
