ZEROFCN Function
Finds the real zeros of a real function using Müller’s method.
Usage
result = ZEROFCN(f)
Input Parameters
f—Scalar string specifying a user-supplied function for which the zeros are to be found. The f function accepts one scalar parameter from which the function is evaluated and returns a scalar of the same type.
Returned Value
result—An array containing the zeros x of the function.
Input Keywords
Double—If present and nonzero, double precision is used.
N_Roots—Number of roots for ZEROFCN to find. Default: N_Roots = 1
XGuess—Array with N_Roots components containing the initial guesses for the zeros. Default: XGuess = 0
Err_Abs—First stopping criterion. A zero, xi, is accepted if | f (xi) | < Err_Abs. Default: Err_Abs = SQRT(ε), where ε is the machine precision
Err_Rel—Second stopping criterion. A zero, xi, is accepted if the relative change of two successive approximations to xi is less than Err_Rel. Default: Err_Rel = SQRT(ε), where ε is the machine precision
Eta—Spread criteria for multiple zeros. If the zero, xi, has been computed and | xi – xj | < Eps, where xj is a previously computed zero, then the computation is restarted with a guess equal to xi + Eta. Default: Eta = 0.01
Eps—See Eta. Default: Eps = SQRT(ε), where ε is the machine precision
Itmax—Maximum number of iterations per zero. Default: Itmax = 100
Info—Array of length N_Roots containing convergence information. The value Info (j – 1) is the number of iterations used in finding the jth zero when convergence is achieved. If convergence is not obtained in Itmax iterations, Info (j – 1) is greater than Itmax.
Discussion
Function ZEROFCN computes n real zeros of a real function f. Given a user-supplied function f (x) and an n-vector of initial guesses x0, x1, ..., xn–1, the function uses Müller’s method to locate n real zeros of f. The function has two convergence criteria. The first criterion requires that | f (xi(m)) | be less than Err_Abs. The second criterion requires that the relative change of any two successive approximations to an xi be less than Err_Rel. Here, xi(m) is the m-th approximation to xi. Let Err_Abs be denoted by ε1, and Err_Rel be denoted by ε2. The criteria can be stated mathematically as follows:
ZEROFCN has two convergence criteria; “convergence” is the satisfaction of either criterion.
Criterion 1:
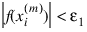
Criterion 2:
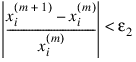
“Convergence” is the satisfaction of either criterion.
Example
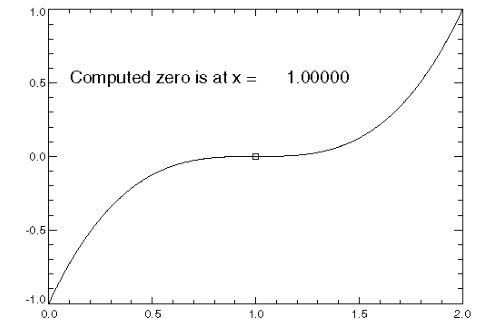
This example finds a real zero of the third-degree polynomial:
f(x) = x3 – 3x2 + 3x – 1
The results are shown in Figure 8-1: ZEROFCN Function.
.RUN
; Define function f.
FUNCTION f, x
RETURN, x^3 - 3 * x^2 + 3 * x - 1
END
; Use hardware characters for the plot.
!P.Font = 0
; Compute the real zero(s).
zero = ZEROFCN('f')x = 2 * FINDGEN(100)/99
; Plot results.
PLOT, x, f(x)
OPLOT, [zero], [f(zero)], Psym = 6
XYOUTS, .5, .5, 'Computed zero is at x = ' + $
STRING(zero(0)), Charsize = 1.5
 |
Warning Errors
MATH_NO_CONVERGE_MAX_ITER—Function failed to converge within Itmax iterations for at least one of the N_Roots roots.





