LAPLACE_INV Function
Computes the inverse Laplace transform of a complex function.
Usage
result = LAPLACE_INV(f, sigma0, t)
Input Parameters
f—Scalar string specifying the user-supplied function for which the inverse Laplace transform will be computed.
sigma0—An estimate for the maximum of the real parts of the singularities of f. If unknown, set sigma0 = 0.0.
t—One-dimensional array of size n containing the points at which the inverse Laplace transform is desired.
Returned Value
result—One-dimensional array of length n whose ith component contains the approximate value of the inverse Laplace transform at the point t(i).
Input Keywords
Double—If present and nonzero, double precision is used.
Pseudo_Acc—The required absolute uniform pseudo accuracy for the coefficients and inverse Laplace transform values. Default: Pseudo_Acc = SQRT(ε), where ε is machine epsilon
Sigma—The first parameter of the Laguerre expansion. If Sigma is not greater than sigma0, it is reset to sigma0+ 0.7. Default: Sigma = sigma0+ 0.7
Bvalue—The second parameter of the Laguerre expansion. If Bvalue is less than 2.0*(Sigma − sigma0), it is reset to 2.5*(Sigma − sigma0). Default: Bvalue = 2.5*(Sigma − sigma0)
Mtop—An upper limit on the number of coefficients to be computed in the Laguerre expansion. Keyword Mtop must be a multiple of four. Default: Mtop = 1024
Output Keywords
Err_Est—Named variable into which an overall estimate of the pseudo error, Disc_Est + Trunc_Err + Cond_Err is stored. See the Discussion section for details.
Disc_Err—Named variable into which the estimate of the pseudo discretization error is stored.
Trunc_Err—Named variable into which the estimate of the pseudo truncation error is stored.
Cond_Err—Named variable into which the estimate of the pseudo condition error on the basis of minimal noise levels in the function values is stored.
K—Named variable into which the coefficient of the decay function is stored. See the Discussion section for details.
R—Named variable into which the base of the decay function is stored. See the Discussion section for details.
Big_Coef_Log—Named variable into which the logarithm of the largest coefficient in the decay function is stored. See the Discussion section for details.
Small_Coef_Log—Named variable into which the logarithm of the smallest nonzero coefficient in the decay function is stored. See the Discussion section for details.
Indicators—Named variable into which an one-dimensional array of length n containing the overflow/underflow indicators for the computed approximate inverse Laplace transform is stored. Table 7-1: Indicator Meanings shows, for the ith point at which the transform is computed, what Indicators(i) signifies.
Indicators(i) | Meaning |
|---|---|
1 | Normal termination. |
2 | The value of the inverse Laplace transform is too large to be representable. This component of the result is set to NaN. |
3 | The value of the inverse Laplace transform is found to be too small to be representable. This component of the result is set to 0.0. |
4 | The value of the inverse Laplace transform is estimated to be too large, even before the series expansion, to be representable. This component of the result is set to NaN. |
5 | The value of the inverse Laplace transform is estimated to be too small, even before the series expansion, to be representable. This component of the result is set to 0.0. |
Discussion
The function LAPLACE_INV computes the inverse Laplace transform of a complex-valued function. Recall that if f is a function that vanishes on the negative real axis, then the Laplace transform of f is defined by:
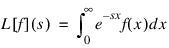
It is assumed that for some value of s the integrand is absolutely integrable.
The computation of the inverse Laplace transform is based on a modification of Weeks’ method (see Weeks (1966)) due to Garbow et al. (1988). This method is suitable when f has continuous derivatives of all orders on [0, ∞). In particular, given a complex-valued function F(s) = L(f) (s), f can be expanded in a Laguerre series whose coefficients are determined by F. This is fully described in Garbow et al. (1988) and Lyness and Giunta (1986).
The algorithm attempts to return approximations g(t) to f(t) satisfying:
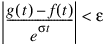
where ε = Pseudo_Acc and σ = Sigma > sigma0. The expression on the left is called the pseudo error. An estimate of the pseudo error is available in Err_Est.
The first step in the method is to transform F to φ where:
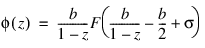
Then, if f is smooth, it is known that φ is analytic in the unit disc of the complex plane and hence has a Taylor series expansion:
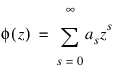
which converges for all z whose absolute value is less than the radius of convergence Rc. This number is estimated in the output keyword R. Using the output keyword K, the smallest number K is estimated which satisfies:
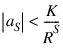
for all R < Rc.
The coefficients of the Taylor series for φ can be used to expand f in a Laguerre series:
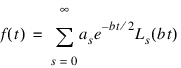
Example 1
This computes the inverse Laplace transform of the function (s – 1)−2, and prints the computed approximation, true transform value, and difference at five points. The correct inverse transform is xex. From Abramowitz and Stegun (1964).
FUNCTION fcn, x
one = COMPLEX(1.0, 0.0)
f = one/((x - one)*(x - 1))
; Return 1/(s - 1)**2
RETURN, f
END
; Initialize t and compute inverse.
n = 5
t = FINDGEN(n) + 0.5
; Compute true inverse, relative difference.
l_inverse = LAPLACE_INV('fcn', 1.5, t)true_inverse = t*EXP(t)
relative_diff = ABS((l_inverse - true_inverse) / true_inverse)
PM, [[t(0:*)], [l_inverse(0:*)], [true_inverse(0:*)], $
[relative_diff(0:*)]], $
Title = ' t f_inv true diff'
This results in the following output:
t f_inv true diff
0.500000 0.824348 0.824361 1.48223e-05
1.50000 6.72247 6.72253 1.01432e-05
2.50000 30.4562 30.4562 2.50504e-07
3.50000 115.906 115.904 1.84310e-05
4.50000 405.053 405.077 5.90648e-05
Example 2
This example computes the inverse Laplace transform of e−1/s/s, and prints the computed approximation, true transform value, and difference at five points. Additionally, the inverse is returned, and a required accuracy for the inverse transform values is specified. The correct inverse transform is:
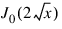
; Return (1/s)(exp(-1/s)
FUNCTION fcn, x
one = COMPLEX(1.0, 0.0)
s_inverse = one / x
f = s_inverse*EXP(-1*(s_inverse))
RETURN, f
END
n = 5
t = FINDGEN(n) + 0.5
l_inverse = LAPLACE_INV('fcn', 0.0, t, $Pseudo_Acc = 1.0e-6, Indicator = indicator)
true_inverse = FLOAT(BESSJ(0, 2.0*SQRT(t)))
relative_diff = ABS((l_inverse - true_inverse) / true_inverse)
FOR i=0L, 4 DO $
IF (indicator(i) EQ 0) THEN $
PM, t(i), l_inverse(i), true_inverse(i), $
relative_diff(i), $
Title = ' t f_inv true diff' $
ELSE $
PRINT, 'Overflow or underflow noted.'
This results in the following output:
t f_inv true diff
0.500000 0.559134 0.559134 1.06602e-07
t f_inv true diff
1.50000 -0.0229669 -0.0229670 4.21725e-06
t f_inv true diff
2.50000 -0.310045 -0.310045 9.61226e-08
t f_inv true diff
3.50000 -0.401115 -0.401115 2.22896e-07
t f_inv true diff
4.50000 -0.370335 -0.370336 4.02369e-07





