CONVOL1D Function
Computes the discrete convolution of two one dimensional arrays.
Usage
result = CONVOL1D(x, y)
Input Parameters
x—One-dimensional array.
y—One-dimensional array.
Returned Value
result—A one-dimensional array containing the discrete convolution of x and y.
Input Keywords
Direct—If present and nonzero, causes the computations to be done by the direct method instead of the FFT method regardless of the size of the vectors passed in.
Periodic—If present and nonzero, then a circular convolution is computed.
Discussion
The function CONVOL1D computes the discrete convolution of two sequences x and y.
Let nx be the length of x, and ny denote the length of y. If keyword Periodic is set, then nz = max{nx, ny}, otherwise nz is set to the smallest whole number, nz ≥ nx + ny – 1, of the form:
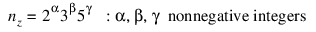
The arrays x and y are then zero-padded to a length nz. Then, we compute:
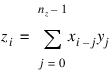
where the index on x is interpreted as a nonnegative number between 0 and nz – 1.
The technique used to compute the zi’s is based on the fact that the (complex discrete) Fourier transform maps convolution into multiplication. Thus, the Fourier transform of z is given by:
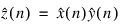
where the following equation is true.
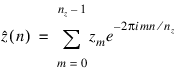
The technique used here to compute the convolution is to take the discrete Fourier transform of x and y, multiply the results together component-wise, and then take the inverse transform of this product. It is very important to make sure that nz is the product of small primes if Periodic is set. If nz is a product of small primes, then the computational effort will be proportional to nz log (nz). If Periodic is not set, then nz is chosen to be a product of small primes.
We point out that if x and y are not complex, then no complex transforms of x or y are taken, since a real transforms can simulate the complex transform above. Such a strategy is six times faster and requires less space than when using the complex transform.
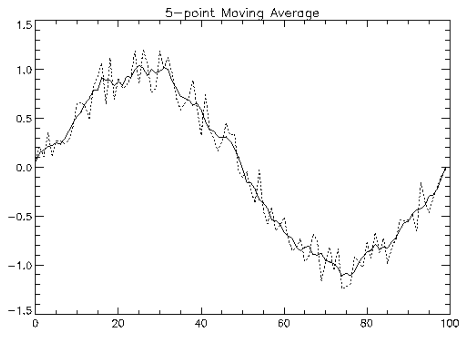
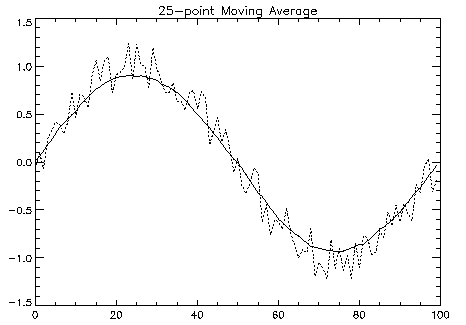
Example
In this example, CONVOL1D is used to compute simple moving-average digital filter plots of 5-point and 25-point moving average filters of noisy data are produced. Results are shown in figures Figure 7-1: 5 Point Moving Average and Figure 7-2: 25 Point Moving Average.
PRO Convol1d_ex1
; Set the random number seed.
RANDOMOPT, SET = 1234579L
ny = 100
t = FINDGEN(ny)/(ny-1)
; Define a 1-period sine wave with added noise.
y = SIN(2*!PI*t) + .5*RANDOM(ny, /Uniform) -.25
; Define the NFLTR-point moving average array.
FOR nfltr=5L, 25, 20 DO BEGIN
nfltr_str = STRCOMPRESS(nfltr,/Remove_All)
fltr = FLTARR(nfltr)
fltr(*) = 1./nfltr
; Convolve filter and signal, using keyword Periodic.
z = CONVOL1D(fltr, y, /Periodic)
PLOT, y, Linestyle=1, Title=nfltr_str + $
'-point Moving Average'
OPLOT, SHIFT(z, -nfltr/2)
ENDFOR
END
 |
 |





