CAT_GLM Function
Analyzes categorical data using logistic, Probit, Poisson, and other generalized linear models.
Usage
result = CAT_GLM(n_class, n_continuous, model, x)
Input Parameters
n_class—Number of classification variables.
n_continuous—Number of continuous variables.
model—Model used to analyze the data. The six models are listed in Table 6-2: Six Models.
model | Relationship* | PDF of Response Variable |
|---|---|---|
0 | Exponential | Poisson |
1 | Logistic | Negative Binomial |
2 | Logistic | Logarithmic |
3 | Logistic | Binomial |
4 | Probit | Binomial |
5 | Log-log | Binomial |
* Relationship between the parameter, θ or λ, and a linear model of the explanatory variables, X β. | ||
note | The lower bound of the response variable is 1 for model = 3 and is 0 for all other models. See the Discussion section for more information about these models. |
x—Two-dimensional array of size n_observations by (n_class + n_continuous) + m containing data for the independent variables, dependent variable, and optional parameters, where n_observations is the number of observations.
The columns must be ordered such that the first n_class columns contain data for the class variables, the next n_continuous columns contain data for the continuous variables, and the next column contains the response variable. The final (and optional) m – 1 columns contain optional parameters, see keywords Ifreq, Ifix, and Ipar.
Returned Value
result—An integer value indicating the number of estimated coefficients in the model.
Input Keywords
Double—If present and nonzero, double precision is used.
Ifreq—Column number Ifreq in x containing the frequency of response for each observation.
Ifix—Column number Ifix in x containing a fixed parameter for each observation that is added to the linear response prior to computing the model parameter. The ‘fixed’ parameter allows one to test hypothesis about the parameters via the log-likelihoods.
Ipar—Column number Ipar in x containing the value of the known distribution parameter for each observation, where x(i, Ipar) is the known distribution parameter associated with the ith observation. The meaning of the distributional parameter depends upon model as shown in Table 6-3: Distributional Parameters:
Model | Parameter | Meaning of parameter (i)(Ipar) |
|---|---|---|
0 | E | ln (E) is a fixed intercept to be included in the linear predictor (i.e., the offset). |
1 | S | Number of successes required for the negative binomial distribution. |
2 | – | Not used for this model. |
3-5 | N | Number of trials required for the binomial distribution. |
Default: When model ≠ 2, each observation is assumed to have a parameter value of 1. When model = 2, this parameter is not referenced.
Eps—Convergence criterion. Convergence is assumed when maximum relative change in any coefficient estimate is less than Eps from one iteration to the next or when the relative change in the log-likelihood, criterion, from one iteration to the next is less than Eps/100.0. Default: Eps = 0.001
Itmax—Maximum number of iterations. Use Itmax = 0 to compute Hessian, stored in Covariances, and the Newton step, stored in Last_Step, at the initial estimates (The initial estimates must be input. Use keyword Init_Est). Default: Itmax = 30
No_Intercept—If present and nonzero, there is no intercept in the model. By default, the intercept is automatically included in the model.
Var_Effects—One-dimensional array of length n_effects containing the number of variables associated with each effect in the model, where n_effects is the number of effects (source of variation) in the model. Keywords Var_Effects and Indicies_Effects must be used together.
Indicies_Effects—One-dimensional index array of length Var_Effects(0) + Var_Effects(1) + ... + Var_Effects(n_effects - 1). The first Var_Effects(0) elements give the column numbers of x for each variable in the first effect. The next Var_Effects(1) elements give the column numbers for each variable in the second effect. The last Var_Effects(n_effects - 1) elements give the column numbers for each variable in the last effect. Keywords Indicies_Effects and Var_Effects must be used together.
Init_Est—One-dimensional array of length n_coef_input containing initial estimates of parameters (n_coef_input can be completed by REGRESSORS). By default, unweighted linear regression is used to obtain initial estimates.
Max_Class—An upper bound on the sum of the number of distinct values taken on by each classification variable. Default: Max_Class = n_observations by n_class
Output Keywords
N_Class_Vals—Named variable into which an one-dimensional array of length n_class containing the number of values taken by each classification variable is stored; the ith classification variable has N_Class_Vals(i) distinct values.
Class_Vals—Named variable into which a one-dimensional array of length:
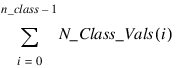
containing the distinct values of the classification variables in ascending order is stored. The first N_Class_Vals(0) elements of Class_Vals contain the values for the first classification variables, the next N_Class_Vals(1) elements contain the values for the second classification variable, etc.
Coef_Stat—Named variable into which a two-dimensional array of size n_coefficients by 4 containing the parameter estimates and associated statistics is stored.
0—Coefficient Estimate.1—Estimated standard deviation of the estimated coefficient.2—Asymptotic normal score for testing that the coefficient is zero.3—The p-value associated with the normal score in column 2.Criterion—Named variable into which the optimized criterion is stored. The criterion to be maximized is a constant plus the log-likelihood.
Covariances—Named variable into which a two-dimensional array of size n_coefficients by n_coefficients containing the estimated asymptotic covariance matrix of the coefficients is stored. For Itmax = 0, this is the Hessian computed at the initial parameter estimates.
Means—Named variable into which an one-dimensional array containing the means of the design variables is stored. The array is of length n_coefficients if keyword No_Intercept is used, and n_coefficients − 1 otherwise.
Case_Analysis—Named variable into which a two-dimensional array of size n_observations by 5 containing the case analysis is stored.
0—Predicted mean for the observation if model = 0. Otherwise, contains the probability of success on a single trial.1—The residual.2—The estimated standard error of the residual.3—The estimated influence of the observation.4—The standardized residual.Case statistics are computed for all observations except where missing values prevent their computation.
Last_Step—Named variable into which an one-dimensional array of length n_coefficients containing the last parameter updates (excluding step halvings) is stored. For Itmax = 0, Last_Step contains the inverse of the Hessian times the gradient vector, all computed at the initial parameter estimates.
Obs_Status—Named variable into which an one-dimensional array of length n_observations indicating which observations are included in the extended likelihood is stored.
0—Observation i is in the likelihood1—Observation i cannot be in the likelihood because it contains at least one missing value in x.2—Observation i is not in the likelihood. Its estimated parameter is infinite.Remarks
1. Dummy variables are generated for the classification variables as follows: An ascending list of all distinct values of each classification variable is obtained and stored in Class_Vals. Dummy variables are then generated for each but the last of these distinct values. Each dummy variable is zero unless the classification variable equals the list value corresponding to the dummy variable, in which case the dummy variable is one. See input keyword Dummy_Method = 1 in routine REGRESSORS.
2. The “product” of a classification variable with a covariate yields dummy variables equal to the product of the covariate with each of the dummy variables associated with the classification variable.
3. The “product” of two classification variables yields dummy variables in the usual manner. Each dummy variable associated with the first classification variable multiplies each dummy variable associated with the second classification variable. The resulting dummy variables are such that the index of the second classification variable varies fastest.
Discussion
Function CAT_GLM uses iteratively reweighted least squares to compute (extended) maximum likelihood estimates in some generalized linear models involving categorized data. One of several models, including the probit, logistic, Poisson, logarithmic, and negative binomial models, may be fit.
Note that each row vector in the data matrix can represent a single observation; or, through the use of keyword Ifreq, each row can represent several observations. Also note that classification variables and their products are easily incorporated into the models via the usual regression-type specifications. The models available in CAT_GLM are listed in Table 6-4: CAT_GLM Models.
Model | PDF of the Response Variable | Parameterization |
|---|---|---|
0 | f (y) = (λy exp (−λ) ) / y! | λ = N × exp (ω + η) |
1 |  |  |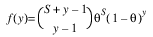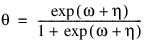
2 |  |  |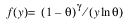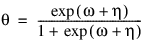
3 |  |  |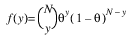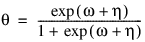
4 | 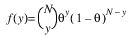 | θ = Φ (ω + η) |
5 | 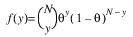 | θ = 1 − exp (−exp (ω + η) ) |
Here, Φ denotes the cumulative normal distribution, N and S are known distribution parameters specified for each observation via the keyword Ipar, and ω is an optional fixed parameter of the linear response, γi, specified for each observation. (If keyword Ifix is not used, then ω is taken to be 0.) Since the log-log model (model = 5) probabilities are not symmetric with respect to 0.5, quantitatively, as well as qualitatively, different models result when the definitions of “success” and “failure” are interchanged in this distribution. In this model and all other models involving θ, θ is taken to be the probability of a “success”.
Computational Details
The computations proceed as follows:
1. The input parameters are checked for consistency and validity.
2. Estimates of the means of the “independent” or design variables are computed. The frequency or the observation in all but binomial distribution models is taken from vector frequencies. In binomial distribution models, the frequency is taken as the product of n = parameter (i) and frequencies (i). Means are computed as:
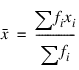
3. By default, unless keyword Init_Est is used, initial estimates of the coefficients are obtained (based upon the observation intervals) as multiple regression estimates relating transformed observation probabilities to the observation design vector. For example, in the binomial distribution models, θ may be estimated as:
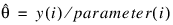
and, when model = 3, the linear relationship is given by:
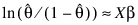
while if model = 4, Φ−1 (θ) = Xβ. When computing initial estimates, standard modifications are made to prevent illegal operations such as division by zero. Regression estimates are obtained at this point, as well as later, by use of function MULTIREGRESS.
4. Newton-Raphson iteration for the maximum likelihood estimates is implemented via iteratively re-weighted least squares. Let:
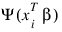
denote the log of the probability of the ith observation for coefficients β. In the least-squares model, the weight of the ith observation is taken as the absolute value of the second derivative of:
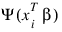
with respect to:
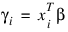
(times the frequency of the observation), and the dependent variable is taken as the first derivative Ψ with respect to γi, divided by the square root of the weight times the frequency. The Newton step is given by:
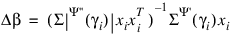
where all derivatives are evaluated at the current estimate of γ and
βn+1 = β – Δβ. This step is computed as the estimated regression coefficients in the least-squares model. Step halving is used when necessary to ensure a decrease in the criterion.
βn+1 = β – Δβ. This step is computed as the estimated regression coefficients in the least-squares model. Step halving is used when necessary to ensure a decrease in the criterion.
5. Convergence is assumed when the maximum relative change in any coefficient update from one iteration to the next is less than Eps or when the relative change in the log-likelihood from one iteration to the next is less than Eps/100. Convergence is also assumed after Itmax iterations or when step halving leads to a step size of less than 0.0001 with no increase in the log-likelihood.
6. Residuals are computed according to methods discussed by Pregibon (1981). Let li (γi ) denote the log-likelihood of the ith observation evaluated at γi. Then, the standardized residual is computed as:
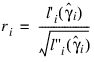
where:
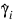
is the value of γi when evaluated at the optimal:
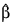
The denominator of this expression is used as the “standard error of the residual” while the numerator is “raw” residual. Following Cook and Weisberg (1982), the influence of the ith observation is assumed to be:
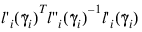
This is a one-step approximation to the change in estimates when the ith observation is deleted. Here, the partial derivatives are with respect to β.
Programming Notes
1. Indicator (dummy) variables are created for the classification variables using function REGRESSORS using keyword Dummy_Method = 1.
2. To enhance precision, “centering” of covariates is performed if the model has an intercept and n_observations − Nmissing > 1. In doing so, the sample means of the design variables are subracted from each observation prior to its inclusion in the model. On convergence, the intercept, its variance, and its covariance with the remaining estimates are transformed to the uncentered estimate values.
3. Two methods for specifying a binomial distribution model are possible. In the first method, Ifreq contains the frequency of the observation while x(i, irt-1) is 0 or 1 depending upon whether the observation is a success or failure. In this case, x(i, n_class + n_ continuous) is always 1. The model is treated as repeated Bernoulli trials, and interval observations are not possible. A second method for specifying binomial models is to use to represent the number of successes in parameter (i) trials. In this case, frequencies will usually be 1.
Example 1
This example is from Prentice (1976) and involves mortality of beetles after five hours exposure to eight different concentrations of carbon disulphide. The table below lists the number of beetles exposed (N) to each concentration level of carbon disulphide (x, given as log dosage) and the number of deaths which result (y). The data is shown in Table 6-5: Beetle Mortality:
Log Dosage | Number of Beetles Exposed | Number of Deaths |
|---|---|---|
1.690 | 59 | 6 |
1.724 | 60 | 13 |
1.755 | 62 | 18 |
1.784 | 56 | 28 |
1.811 | 63 | 52 |
1.836 | 59 | 53 |
1.861 | 62 | 61 |
1.883 | 60 | 60 |
The number of deaths at each concentration level are fitted as a binomial response using logit (model = 3), probit (model = 4), and log-log (model = 5) models. Note that the log-log model yields a smaller absolute log likelihood (14.81) than the logit model (18.78) or the probit model (18.23). This is to be expected since the response curve of the log-log model has an asymmetric appearance, but both the logit and probit models are symmetric about θ = 0.5.
PRO print_results, cs, means, ca, crit, ls, cov
PRINT, ' Coefficient Satistics'
PRINT, ' Standard Asymptotic ', $
'Asymptotic'
PRINT, ' Coefficient Error Z-statistic ', $
'P-value'
PM, cs, Format = '(4F13.2)'
PRINT, 'Covariate Means = ', means, Format = '(A18, F6.3)'
PRINT, ' Case Analysis'
PRINT, ' Residual ', $
'Standardized'
PRINT, ' Predicted Residual Std. Error Leverage', $
' Residual'
PM, ca, Format = '(5F12.3)'
PRINT, 'Log-Likelihood = ', crit, Format = '(A18, F9.5)'
PRINT, ' Last Step'
PRINT, ls
PRINT, 'Asymptotic Coefficient Covariance'
PM, cov, Format = '(2F12.4)'
END
model = 3
nobs = 8
x = ([[1.690, 1.724, 1.755, 1.784, 1.811, 1.836, 1.861, 1.883], $
[6, 13, 18, 28, 52, 53, 61, 60], $
[59, 60, 62, 56, 63, 59, 62, 60]])
ncoef = CAT_GLM(0, 1, model, x, Ipar = 2, Eps = 1.0e-3, $
Coef_Stat = cs, Covariances = cov, Criterion = crit, $
Means = means, Case_Analysis = ca, Last_Step = ls, $
Obs_Status = os)
This results in the following output:
print_results, cs, means, ca, crit, ls, cov
Coefficient Satistics
Standard Asymptotic Asymptotic
Coefficient Error Z-statistic P-value
-60.76 5.21 -11.66 0.00
34.30 2.92 11.76 0.00
Covariate Means = 1.793
Case Analysis
Residual Standardized
Predicted Residual Std. Error Leverage Residual
0.058 2.593 1.792 0.267 1.448
0.164 3.139 2.871 0.347 1.093
0.363 -4.498 3.786 0.311 -1.188
0.606 -5.952 3.656 0.232 -1.628
0.795 1.890 3.202 0.269 0.590
0.902 -0.195 2.288 0.238 -0.085
0.956 1.743 1.619 0.198 1.077
0.979 1.278 1.119 0.138 1.143
Log-Likelihood = -18.77818
Last Step
-3.67824e-08 1.04413e-05
Asymptotic Coefficient Covariance
27.1368 -15.1243
-15.1243 8.5052
Warning Errors
STAT_TOO_MANY_HALVINGS—Too many step halvings. Convergence is assumed.
STAT_TOO_MANY_ITERATIONS—Too many iterations. Convergence is assumed.
Fatal Errors
STAT_TOO_FEW_COEF—Init_Est is used and “n_coef_input” = #. The model specified requires # coefficients.
STAT_MAX_CLASS_TOO_SMALL—The number of distinct values of the classification variables exceeds “Max_Class” = #.
STAT_INVALID_DATA_8—“N_Class_Values(#)” = #. The number of distinct values for each classification variable must be greater than one.
STAT_NMAX_EXCEEDED—The number of observations to be deleted has exceeded “lp_max” = #. Rerun with a different model or increase the workspace.
