CONTINGENCY Function
Performs a chi-squared analysis of a two-way contingency table.
Usage
result = CONTINGENCY(table)
Input Parameters
table—Two-dimensional array containing the observed counts in the contingency table.
Returned Value
result—Pearson chi-squared p-value for independence of rows and columns.
Input Keywords
Double—If present and nonzero, double precision is used.
Output Keywords
Chi_Sq_Test—Named variable into which the three-element array containing statistics associated with the chi-squared tests is stored. The first element contains the degrees of freedom for the chi-squared tests associated with the table, the second element contains the Pearson chi-squared test statistic, and the third element contains the probability of a larger Pearson chi-squared, p‑value.
Lrt—Named variable into which the three-element array containing statistics associated with the likelihood ratio G-squared tests is stored. The first element contains the degrees of freedom for the chi-squared tests associated with the table, the second element contains the likelihood ratio G2 (chi-squared), and the third element contains the probability of a larger G2.
Expected—Named variable into which the two-dimensional array of size (n_rows+1) by (n_columns+1) containing the expected values of each cell in the table is stored, where n_rows=(N_ELEMENTS(table(*,0)) and n_columns=(N_ELEMENTS(table(0,*)). The expected values are computed under the null hypothesis and stored in the first n_rows rows and n_columns columns. The marginal totals are in the last row and column.
Chi_Sq_Contrib—Named variable into which a two-dimensional array of size (n_rows+1) by (n_columns+1) containing the contributions for each cell in the table is stored. The contributions to chi-squared for each cell in the table is in the first n_rows rows and n_columns columns. The last row and column contain the total contribution to chi-squared for that row or column.
Chi_Sq_Stats—Named variable into which an array of length 5 containing chi-squared statistics associated with this contingency table is stored. The last three elements are based on Pearson’s chi-squared statistic (see Chi_Sq_Test). The chi-squared statistics are given as follows:
Table_Stats—Named variable into which a two-dimensional array of size 23 × 5 containing statistics associated with this table is stored. Each row corresponds to a statistic, as shown in Table 6-1: Row Statistics.
Row | Statistic |
|---|---|
0 | Gamma |
1 | Kendall’s τb |
2 | Stuart’s τc |
3 | Somers’ D for rows (given columns) |
4 | Somers’ D for columns (given rows) |
5 | product moment correlation |
6 | Spearman rank correlation |
7 | Goodman and Kruskal τ for rows (given columns) |
8 | Goodman and Kruskal τ for columns (given rows) |
9 | uncertainty coefficient U (symmetric) |
10 | uncertainty Ur|c (rows) |
11 | uncertainty U c|r (columns) |
12 | optimal prediction λ (symmetric) |
13 | optimal prediction λ r|c (rows) |
14 | optimal prediction λ c|r (columns) |
15 | optimal prediction λ r|c (rows) |
16 | optimal prediction λ c|r (columns) |
17 | test for linear trend in row probabilities if n_rows = 2. If n_rows is not 2, a test for linear trend in column probabilities if n_columns = 2. |
18 | Kruskal-Wallis test for no-row effect |
19 | Kruskal-Wallis test for no-column effect |
20 | kappa (square tables only) |
21 | McNemar test of symmetry (square tables only) |
22 | McNemar one degree of freedom test of symmetry (square tables only) |
If a statistic cannot be computed or if some value is not relevant for the computed statistic, the entry is NaN (Not a Number). The columns are as follows:
In the McNemar tests, Column 0 contains the statistic, Column 1 contains the chi-squared degrees of freedom, Column 3 contains the exact p-value (1 degree of freedom only), and Column 4 contains the chi-squared asymptotic p-value. The Kruskal-Wallis test is the same except no exact p-value is computed.
Discussion
Function CONTINGENCY computes statistics associated with an r × c contingency table. The function computes the chi-squared test of independence, expected values, contributions to chi-squared, row and column marginal totals, some measures of association, correlation, prediction, uncertainty, the McNemar test for symmetry, a test for linear trend, the odds and the log odds ratio, and the kappa statistic (if the appropriate keywords are selected).
Notation
Let xij denote the observed cell frequency in the ij cell of the table and n denote the total count in the table. Let pij = pi·p·j denote the predicted cell probabilities under the null hypothesis of independence, where pi· and p·j are the row and column marginal relative frequencies. Next, compute the expected cell counts as eij = npij.
Also required in the following are auv and buv for u, where ν = 1, ..., n. Let (rs, cs) denote the row and column response of observation s. Then, auv = 1, 0, or –1, depending on whether ru < rv , ru = rv , or ru > rv. The buv similarly defined in terms of the cs variables.
Chi-squared Statistic
For each cell in the table, the contribution to χ2 is given as (xij – eij)2/eij. The Pearson chi-squared statistic (denoted χ2) is computed as the sum of the cell contributions to chi-squared. It has (r – 1) (c – 1) degrees of freedom and tests the null hypothesis of independence, i.e., H0:pij = pi·p·j. The null hypothesis is rejected if the computed value of χ2 is too large.
The maximum likelihood equivalent of χ2, G2 is computed as follows:
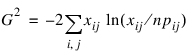
G2 is asymptotically equivalent to χ2 and tests the same hypothesis with the same degrees of freedom.
Measures Related to Chi-squared (Phi, Contingency Coefficient, and Cramer’s V)
There are three measures related to chi-squared that do not depend on sample size:
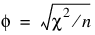
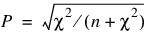
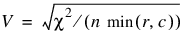
Since these statistics do not depend on sample size and are large when the hypothesis of independence is rejected, they can be thought of as measures of association and can be compared across tables with different sized samples. While both P and V have a range between 0.0 and 1.0, the upper bound of P is actually somewhat less than 1.0 for any given table (see Kendall and Stuart 1979, p. 587). The significance of all three statistics is the same as that of the χ2 statistic, Chi_Sq_Test.
The distribution of the χ2 statistic in finite samples approximates a chi-squared distribution. To compute the exact mean and standard deviation of the χ2 statistic, Haldane (1939) uses the multinomial distribution with fixed-table marginals. The exact mean and standard deviation generally differ little from the mean and standard deviation of the associated chi-squared distribution.
Standard Errors and p-values for Some Measures of Association
In Columns 1 through 4 of statistics, estimated standard errors and asymptotic p-values are reported. Estimates of the standard errors are computed in two ways. The first estimate, in Column 1 of the array table_stats, is asymptotically valid for any value of the statistic. The second estimate, in Column 2 of the array, is only correct under the null hypothesis of no association. The z-scores in Column 3 of statistics are computed using this second estimate of the standard errors. The p-values in column 4 are computed from this z-score. See Brown and Benedetti (1977) for a discussion and formulas for the standard errors in Column 2.
Measures of Association for Ranked Rows and Columns
The measures of association, φ, P, and V, do not require any ordering of the row and column categories. Function CONTINGENCY also computes several measures of association for tables in which the row and column categories correspond to ranked observations. Two of these tests, the product moment correlation and the Spearman correlation, are correlation coefficients computed using assigned scores for the row and column categories. The cell indices are used for the product-moment correlation, while the average of the tied ranks of the row and column marginals is used for the Spearman rank correlation. Other scores are possible.
Gamma, Kendall’s τb, Stuart’s τc, and Somers’ D are measures of association that are computed like a correlation coefficient in the numerator. In all these measures, the numerator is computed as the “covariance” between the auv variables and buv variables defined above, i.e., as follows:
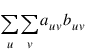
Recall that auv and buv can take values –1, 0, or 1. Since the product auvbuv = 1 only if auv and buv are both 1 or both –1, it is easy to show that this “covariance” is twice the total number of agreements minus the number of disagreements, where a disagreement occurs when auvbuv = –1.
Kendall’s τb is computed as the correlation between auv and buv variables (see Kendall and Stuart 1979, p. 593). In a rectangular table (r ≠ c), Kendall’s τb cannot be 1.0 (if all marginal totals are positive). For this reason, Stuart suggested a modification to the denominator of τ in which the denominator becomes the largest possible value of the “covariance.” This maximizing value is approximately n2m / (m – 1), where m = min(r, c). Stuart’s τc uses this approximate value in its denominator. For large n:
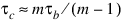
Gamma can be motivated in a slightly different manner. Because the “covariance” of the auv variables and the buv variables can be thought of as twice the number of agreements minus the disagreements, 2(A – D), where A is the number of agreements and D is the number of disagreements, Gamma is motivated as the probability of agreement minus the probability of disagreement, given that either agreement or disagreement occurred. This is shown as γ = (A – D)/(A + D).
Two definitions of Somers’ D are possible, one for rows and a second for columns. Somers’ D for rows can be thought of as the regression coefficient for predicting auv from buv. Moreover, Somer’s D for rows is the probability of agreement minus the probability of disagreement, given that the column variable, buv, is not 0. Somers’ D for columns is defined in a similar manner.
A discussion of all of the measures of association in this section can be found in Kendall and Stuart (1979, p. 592).
Measures of Prediction and Uncertainty
Optimal Prediction Coefficients: The measures in this section do not require any ordering of the row or column variables. They are based entirely upon probabilities. Most are discussed in Bishop et al. (1975, p. 385).
Consider predicting (or classifying) the column for a given row in the table. Under the null hypothesis of independence, choose the column with the highest column marginal probability for all rows. In this case, the probability of misclassification for any row is 1 minus this marginal probability. If independence is not assumed, then within each row, choose the column with the highest row-conditional probability. The probability of misclassification for the row becomes 1 minus this conditional probability.
Define the optimal prediction coefficient λc | r for predicting columns from rows as the proportion of the probability of misclassification that is eliminated because the random variables are not independent. It is estimated by:
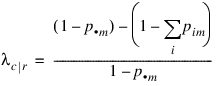
where m is the index of the maximum estimated probability in the row (pim) or row margin (p·m). A similar coefficient is defined for predicting the rows from the columns. The symmetric version of the optimal prediction λ is obtained by summing the numerators and denominators of λr|c and λc|r, then dividing. Standard errors for these coefficients are given in Bishop et al. (1975, p. 388).
A problem with the optimal prediction coefficients λ is that they vary with the marginal probabilities. One way to correct this is to use row-conditional probabilities. The optimal prediction λ* coefficients are defined as the corresponding λ coefficients in which first the row (or column) marginals are adjusted to the same number of observations. This yields:
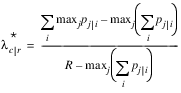
where i indexes the rows, j indexes the columns, and p j|i is the (estimated) probability of column j given row i. λ*r|c is similarly defined.
Goodman and Kruskal τ: A second kind of prediction measure attempts to explain the proportion of the explained variation of the row (column) measure given the column (row) measure. Define the total variation in the rows as follows:
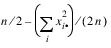
Note that this is 1 / (2n) times the sums of squares of the auv variables.
With this definition of variation, the Goodman and Kruskal τ coefficient for rows is computed as the reduction of the total variation for rows accounted for by the columns, divided by the total variation for the rows. To compute the reduction in the total variation of the rows accounted for by the columns, note that the total variation for the rows within column j is defined as follows:
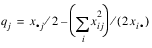
The total variation for rows within columns is the sum of the qj variables. Consistent with the usual methods in the analysis of variance, the reduction in the total variation is given as the difference between the total variation for rows and the total variation for rows within the columns.
Goodman and Kruskal’s τ for columns is similarly defined. See Bishop et al. (1975, p. 391) for the standard errors.
Uncertainty Coefficients: The uncertainty coefficient for rows is the increase in the log-likelihood that is achieved by the most general model over the independence model, divided by the marginal log-likelihood for the rows. This is given by the following equation:
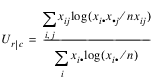
The uncertainty coefficient for columns is similarly defined. The symmetric uncertainty coefficient contains the same numerator as Ur | c and Uc | r but averages the denominators of these two statistics. Standard errors for U are given in Brown (1983).
Kruskal-Wallis: The Kruskal-Wallis statistic for rows is a one-way analysis-of-variance-type test that assumes the column variable is monotonically ordered. It tests the null hypothesis that no row populations are identical, using average ranks for the column variable. The Kruskal-Wallis statistic for columns is similarly defined. Conover (1980) discusses the Kruskal-Wallis test.
Test for Linear Trend: When there are two rows, it is possible to test for a linear trend in the row probabilities if it is assumed that the column variable is monotonically ordered. In this test, the probabilities for row 1 are predicted by the column index using weighted simple linear regression. This slope is given by:
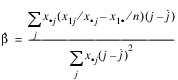
where:
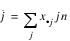
is the average column index. An asymptotic test that the slope is zero may then be obtained (in large samples) as the usual regression test of zero slope.
In two-column data, a similar test for a linear trend in the column probabilities is computed. This test assumes that the rows are monotonically ordered.
Kappa: Kappa is a measure of agreement computed on square tables only. In the kappa statistic, the rows and columns correspond to the responses of two judges. The judges agree along the diagonal and disagree off the diagonal. Let:
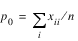
denote the probability that the two judges agree, and let
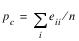
denote the expected probability of agreement under the independence model. Kappa is then given by (p0 – pc)/(1 – pc).
McNemar Tests: The McNemar test is a test of symmetry in a square contingency table. In other words, it is a test of the null hypothesis H0:θij = θji . The multiple degrees-of-freedom version of the McNemar test with r(r – 1)/2 degrees of freedom is computed as follows:
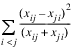
The single degree-of-freedom test assumes that the differences, xij – xji , are all in one direction. The single degree-of-freedom test is more powerful than the multiple degrees-of-freedom test when this is the case. The test statistic is given as follows:
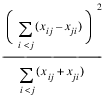
The exact probability can be computed by the binomial distribution.
Example 1
The following example, taken from Kendall and Stuart (1979), involves the distance vision in the right and left eyes. Output contains only the p-value.
table = [[821,116,72,43], [112,494,151,34], $
[85,145,583,106], [35,27,87,331]]
print, 'P-Value ', CONTINGENCY(table)
Example 2
The following example, which illustrates the use of Kappa and McNemar tests, uses the same distance vision data as the previous example. The available statistics are obtained using keywords. First, a procedure is defined to output the results.
note | To run this example, use the .RUN command and then copy and paste this example into PV‑WAVE. |
PRO print_results, chi_sq_test, lrt, expected, chi_sq_contrib, $
chi_sq_stats, table_stats
PRINT, 'Pearson Chi_Squared Statistics:'
PM, chi_sq_test(0), Title = 'Degrees of Freedom'
PM, chi_sq_test(1), Title = 'Chi-Squared'
PM, chi_sq_test(2), Title = 'P-Value'
PRINT, 'Likelihood Ratio G-Squared ' + 'Statistics:'
PM, lrt(0), Title = 'Degrees of Freedom'
PM, lrt(1), Title = 'G-Squared'
PM, lrt(2), Title = 'P-Value'
PM, expected, Title = 'Expected Values:'
PM, chi_sq_contrib, Title = 'Contributions to Chi-squared:'
PM, chi_sq_stats, Title = 'Chi-square Statistics:'
PM, table_stats, Title = 'Table Statistics:'
END
table = [[821,116,72,43], [112,494,151,34], [85,145,583,106], $
[35,27,87,331]]
p_value = CONTINGENCY(table, $
Chi_Sq_Test = chi_sq_test, $
Lrt = lrt, $
Expected = expected, $
Chi_Sq_Contrib = chi_sq_contrib, $
Chi_Sq_Stats = chi_sq_stats, $
Table_Stats = table_stats)
print_results, chi_sq_test, lrt, expected, chi_sq_contrib, $
chi_sq_stats, table_stats
This results in the following output:
Pearson Chi_Squared Statistics:
Degrees of Freedom
9.00000
Chi-Squared
3304.37
P-Value
0.00000
Likelihood Ratio G-Squared Statistics:
Degrees of Freedom
9.00000
G-Squared
2781.02
P-Value
0.00000
Expected Values:
341.689 256.916 298.491 155.904 1053.00
253.752 190.796 221.671 115.780 782.000
289.771 217.879 253.136 132.215 893.000
166.788 125.408 145.702 76.1012 514.000
1052.00 791.000 919.000 480.000 3242.00
Contributions to Chi-squared:
672.363 81.7416 152.696 93.7612 1000.56
74.7802 481.835 26.5189 68.0768 651.211
163.661 20.5287 429.849 15.4625 629.501
91.8743 66.6263 10.8183 853.777 1023.10
1002.68 650.732 619.882 1031.08 3304.37
Chi-square Statistics:
9.00278
4.24016
1.00957
0.710467
0.582877
Table Statistics:
0.775704 0.0122983 0.0148632 52.1897 0.000000
0.642887 0.0122028 0.0123183 52.1897 0.000000
0.629265 0.0120573 1.#QNAN 52.1897 0.000000
0.641831 0.0122390 0.0122980 52.1897 0.000000
0.643945 0.0122152 0.0123385 52.1897 0.000000
0.692588 0.0127669 0.0172000 40.2669 0.000000
0.693882 0.0126566 0.0126942 54.6614 0.000000
0.341952 0.0122570 1.#QNAN 1.#QNAN 1.#QNAN
0.342993 0.0122165 1.#QNAN 1.#QNAN 1.#QNAN
0.317123 0.0110281 1.#QNAN 1.#QNAN 1.#QNAN
0.317811 0.0110453 1.#QNAN 1.#QNAN 1.#QNAN
0.316437 0.0110294 1.#QNAN 1.#QNAN 1.#QNAN
0.537337 0.0123718 1.#QNAN 1.#QNAN 1.#QNAN
0.537443 0.0125727 1.#QNAN 1.#QNAN 1.#QNAN
0.537232 0.0125851 1.#QNAN 1.#QNAN 1.#QNAN
0.550648 0.0135695 1.#QNAN 1.#QNAN 1.#QNAN
0.563587 0.0126838 1.#QNAN 1.#QNAN 1.#QNAN
1.#QNAN 1.#QNAN 1.#QNAN 1.#QNAN 1.#QNAN
1561.49 3.00000 1.#QNAN 1.#QNAN 0.000000
1563.03 3.00000 1.#QNAN 1.#QNAN 0.000000
0.574419 0.0110873 0.0105673 54.3583 0.000000
4.76249 6.00000 1.#QNAN 1.#QNAN 0.574617
0.948667 1.00000 1.#QNAN 0.345904 0.330059
Warning Errors
STAT_DF_GT_30—The degrees of freedom for Chi_Sq_Test are greater than 30. The exact mean, standard deviation, and the normal distribution function should be used.
STAT_EXP_VALUES_TOO_SMALL—Some expected values are less than #. Some asymptotic p-values may not be good.
STAT_PERCENT_EXP_VALUES_LT_5—Twenty percent of the expected values are calculated less than 5.





