RCBD_FACTORIAL Function
Analyzes data from balanced and unbalanced randomized complete-block experiments. Unlike ANOVAFACT, RCBD_FACTORIAL allows for missing data, unequal replication and one or more locations.
Usage
result = RCBD_FACTORIAL (n_obs, n_locations, n_factors, n_levels, model, y)
Input Parameters
n_obs—Number of missing and non-missing experimental observations.
n_locations—Number of locations. n_locations must be one or greater.
n_factors—Number of factors in the model.
n_levels—Array of length n_factors + 1. The n_levels(0) through n_levels(n_factors – 1) contain the number of levels for each factor. The last element, n_levels(n_factors), contains the number of blocks at a location. There must be at least two blocks and two levels for each factor, i.e., n_levels(i) > 2 for i=0, 1, …, n_factors.
model—An n_obs by (n_factors + 2) array identifying the location, block and factor levels associated with each observation in y. The first column must contain the location identifier and the second column must contain the block identifier for the observation associated with that row. The remaining columns, columns 3 through n_factors + 2, should contain the factor level identifiers in the same order used in n_levels. If n_locations = 1, the first column is still required, but its contents are ignored.
y—Array of length n_obs containing the experimental observations and any missing values. Missing values cannot be omitted. They are indicated by placing a NaN (Not a Number) at the appropriate positions in y. NaN can be defined by calling the MACHINE function. For example:
x = MACHINE(/Float)
y(i) = x.NaN
Returned Value
result—A two dimensional, N_anova by 6 array containing the ANOVA table, where:
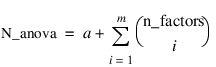
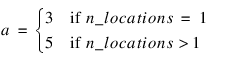
and m= n_factors.
Each row in this array contains values for one of the effects in the ANOVA table. The first value in each row, anova_tablei,0 = anova_table(i,0), is the source identifier which identifies the type of effect associated with values in that row. The remaining values in a row contain the ANOVA table values shown in Table 5-32: ANOVA Table Values.
J | anova_tablei,j = anova_table(i,j) |
0 | Source Identifier (values described below) |
1 | Degrees of freedom |
2 | Sum of squares |
3 | Mean squares |
4 | F-statistic |
5 | p-value for this F-statistic |
The values for the mean squares, F-statistic and p-value are set to NaN for the residual and corrected total effects.
The Source Identifiers in the first column of anova_tablei,j are the only negative values in anova_table. The absolute value of the source identifier is equal to the order of the effect in that row. Main effects, for example, have a source identifier of –1. Two-way interactions use a source identifier of –2, –3 and so on.
Source Identifier | ANOVA Source |
–1 | Main Effects1 |
–2 | Two-Way Interactions2 |
–3 | Three-Way Interactions2 |
. . . | . . . |
–n_factors | (n_factors)-way Interactions2 |
–n_factors-1 | Effects Error Term |
–n_factors-2 | Residual3 |
–n_factors-3 | Corrected Total |
Notes: 1. Number of main effects is equal to n_factors + 2 if n_locations > 1, and n_factors + 1 if n_locations = 1. The first two rows, anova_table(0,*) through anova_table(1,*) are used to represent the location and block effects if n_locations > 1. If n_locations = 1, then anova_table(0,*) contain the block effects. 2. The number of interaction effects for the nth-way interactions is equal to: 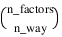 The order of these terms is in ascending order by treatment subscript. The interactions for factor 1 appear first, followed by factor 2, factor 3, and so on. 3. The residual term is only provided when there is replication within blocks. | |
note | The Effects Error Term is equal to the Residual effect if n_locations = 1. |
Output Keywords
N_missing—Number of missing values, if any, found in y. Missing values are denoted with a NaN (Not a Number) value.
Cv—Coefficient of Variation computed by:
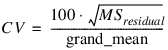
Grand_mean—Mean of all the data across every location.
Factor_means—Array of length n_levels(0) + n_levels(1) + … + n_levels(n_factors – 1) containing the factor means.
Factor_std_errors—An n_factors by 2 array containing factor standard errors and their associated degrees of freedom. The first column contains the standard errors for comparing two factor means and the second its associated degrees of freedom.
Two_way_means—One-dimensional array containing the two-way means for all two by two combinations of the factors. If n_factors = 1 this keyword is not valid. The total length of this array when n_factors > 1 is equal to:
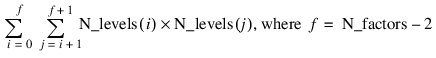
If n_factors > 1, the means would first be produced for all combinations of the first two factors followed by all combinations of the remaining factors using the subscript order suggested by the above formula. For example, if the experiment is a 2x2x2 factorial, the 12 two-way means would appear in the following order: A1B1, A1B2, A2B1, A2B2, A1C1, A1C2, A2C1, A2C2, B1C1, B1C2, B2C1, and B2C2.
Two_way_std_errors—An N_two_way by 2 array containing factor standard errors and their associated degrees of freedom, where:
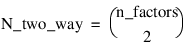
The first column contains the standard errors for comparing two 2-way interaction means and the second its associated degrees of freedom. The ordering of the rows in this array is similar to that used in two_way_means. For example if n_factors = 4, then N_two_way = 6 with the order AB, AC, AD, BC, BD, CD.
Treatment_means—Array of size:
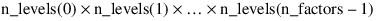
containing the treatment means. The order of the means is organized in ascending order by the value of the factor identifier. containing the treatment means. The order of the means is organized in ascending order by the value of the factor identifier. For example, if the experiment is a 2x2x2 factorial, the 8 means would appear in the following order: A1B1C1, A1B1C2, A1B2C1, A1B1C2, A2B1C1, A2B1C2, A2B2C1, and A2B2C2.
Treatment_std_errors—The array of length 2 containing standard error for comparing treatments based upon the average number of replicates per treatment and its associated degrees of freedom.
Anova_row_labels—An array containing the labels for each of the rows of the returned ANOVA table. The label for the ith row of the ANOVA table can be printed with PRINT, Anova_row_labels(i).
Double—If present and nonzero, double precision is used.
Discussion
RCBD_FACTORIAL is capable of analyzing randomized complete block factorial experiments replicated in different locations. Missing observations are estimated using the Yates method. Locations, if used, and blocks are treated as random factors. All treatment factors are regarded as fixed effects in the analysis. If n_locations > 1, then blocks are treated as nested within locations and the number of blocks used at each location must be the same.
If n_locations = 1, then the residual mean square is used as the error mean square in calculating the F-tests for all other effects. That is:
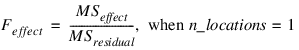
In this case, the residual mean square is calculating by pooling all interactions between treatments and blocks. For example, if treatments are formed from two factors, A and B, then:

When n_locations = 1, then MSresidual is also used to calculate the standard errors between means. For example, in a two factor experiment:
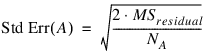
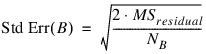
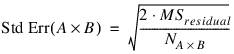
where NA, NB, and NA×B are the number of observations for each level of the effects A, B and their interaction, respectively.
If n_locations > 1, then the error mean square is used as the denominator of the F-test for effects:
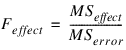
The error mean square in this calculation is obtained by pooling all interactions between each factor and locations. For example n_locations > 1 and n_factors = 2 then:
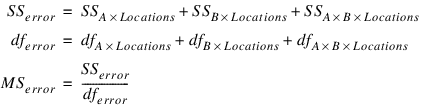
In this case, n_locations > 1, the standard errors for means are calculated using
MSerror instead of MSresidual
The F-test for differences between locations is calculated using the mean squares for blocks within locations:
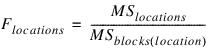
Example
This example is based upon data from an agricultural trial conducted by DOW Agrosciences. This is a three factor, 3x2x2, experiment replicated in two blocks at one location. For illustration, two observations are set to NaN to simulate missing observations.
n_obs = 24
n_locations = 1
n_factors = 3
n_levels = [3, 2, 2, 2]
model = TRANSPOSE([[1, 1, 1, 1, 1], $
[1, 2, 1, 1, 1], $
[1, 1, 1, 1, 2], $
[1, 2, 1, 1, 2], $
[1, 1, 1, 2, 1], $
[1, 2, 1, 2, 1], $
[1, 1, 1, 2, 2], $
[1, 2, 1, 2, 2], $
[1, 1, 2, 1, 1], $
[1, 2, 2, 1, 1], $
[1, 1, 2, 1, 2], $
[1, 2, 2, 1, 2], $
[1, 1, 2, 2, 1], $
[1, 2, 2, 2, 1], $
[1, 1, 2, 2, 2], $
[1, 2, 2, 2, 2], $
[1, 1, 3, 1, 1], $
[1, 2, 3, 1, 1], $
[1, 1, 3, 1, 2], $
[1, 2, 3, 1, 2], $
[1, 1, 3, 2, 1], $
[1, 2, 3, 2, 1], $
[1, 1, 3, 2, 2], $
[1, 2, 3, 2, 2]])
y = [4.42725419998168950, 2.98526261840015650, $
2.12795543670654300, 4.36357164382934570, $
2.55254390835762020, 2.78596709668636320, $
1.21479606628417970, 2.68143519759178160, $
2.47588264942169190, 4.69543695449829100, $
5.01306104660034180, 3.01919978857040410, $
4.73502767086029050, 0.00000000000000000, $
0.00000000000000000, 5.05780076980590820, $
5.01421167794615030, 3.61517095565795900, $
4.11972457170486450, 4.71947982907295230, $
6.51671624183654790, 4.22036057710647580, $
4.73365202546119690, 4.68545144796371460]
a = MACHINE(/Float)
NaN = a.NAN
y(13) = NaN
y(14) = NaN
aov = RCBD_FACTORIAL(n_obs, n_locations, n_factors, $
n_levels, model, y, $
Anova_row_labels=anova_row_labels)
; Print Analysis of Variance Table
PRINT, " *** ANALYSIS OF VARIANCE TABLE ***"
PRINT, 'ID', 'DF', 'SSQ', 'MS', 'F-Test', 'p-Value', $
Format='(A16, A6, A8, A8, A8, A9)'
FOR i=0L, (SIZE(aov))(1)-1 DO $
PRINT, anova_row_labels(i), aov(i,0), aov(i,1), $
aov(i,2), aov(i,3), aov(i,4), aov(i,5), Format= $
'(A11, 2X, I3, 3X, F3.0, 2X, F6.2, 3X, F5.2, 2X, ' + $
'F6.2, 4X, F5.3)'
Output
*** ANALYSIS OF VARIANCE TABLE ***
ID DF SSQ MS F-test P-Value
Blocks -1 1. 0.01 0.01 NaN NaN
[1] -1 2. 14.73 7.37 5.15 0.032
[2] -1 1. 0.24 0.24 0.17 0.692
[3] -1 1. 0.15 0.15 0.10 0.756
[1]x[2] -2 2. 5.79 2.89 2.02 0.188
[1]x[3] -2 2. 1.02 0.51 0.36 0.710
[2]x[3] -2 1. 0.20 0.20 0.14 0.719
[1]x[2]x[3] -3 2. 0.13 0.06 0.05 0.956
Error -4 9. 12.88 1.43 NaN NaN
Total -6 21. 35.15 NaN NaN NaN





