CRD_FACTORIAL Function
Analyzes data from balanced and unbalanced completely randomized experiments. CRD_FACTORIAL does permit a factorial treatment structure. However, unlike ANOVAFACT, CRD_FACTORIAL allows for missing data and one or more locations.
Usage
anova_table = CRD_FACTORIAL (n_obs, n_locations, n_factors, n_levels, model, y)
Input Parameters
n_obs—Number of missing and non-missing experimental observations.
n_locations—Number of locations. n_locations must be one or greater.
n_factors—Number of factors in the model.
n_levels—Array of length n_factors+1. n_levels(0) through n_levels(n_factors – 1) contain the number of levels for each factor. The last element, n_levels(n_factors), contains the number of replicates for each treatment combination within a location.
model—An n_obs by (n_factors+1) array identifying the location and factor levels associated with each observation in y. The first column must contain the location identifier and the remaining columns the factor level identifiers in the same order used in n_levels. If n_locations = 1, the first column is still required, but its contents are ignored.
y—An array of length n_obs containing the experimental observations and any missing values. Missing values cannot be omitted. They are indicated by placing a NaN (Not a Number) at the appropriate positions in y. NaN can be defined by calling the MACHINE function. For example:
x = MACHINE(/Float)
y(i) = x.NaN
Returned Value
anova_table—A two-dimensional, N_anova by 6 array containing the ANOVA table, where:
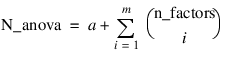
where:
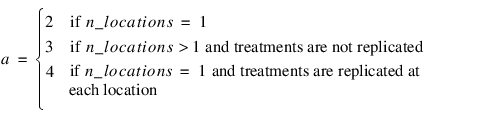
and m = model_order.
Each row in this array contains values for one of the effects in the ANOVA table. The first value in each row, anova_tablei,0 = anova_table(i,0), is the source identifier which identifies the type of effect associated with values in that row. The remaining values in a row contain the ANOVA table values using the convention listed in Table 5-30: ANOVA Table Values:
J | anova_tablei,j = anova_table(i,j) |
|---|---|
0 | Source Identifier (values described below) |
1 | Degrees of freedom |
2 | Sum of squares |
3 | Mean squares |
4 | F-statistic |
5 | p-value for this F-statistic |
The values for the mean squares, F-statistic and p-value are set to NaN for the residual and corrected total effects.
The Source Identifiers in the first column of anova_tablei,j are the only negative values in anova_table. The absolute value of the source identifier is equal to the order of the effect in that row. Main effects, for example, have a source identifier of –1. Two-way interactions use a source identifier of –2, and so on. Refer to Table 5-31: Source Identifiers for a list of Source Identifiers.
Source Identifier | ANOVA Source |
|---|---|
–1 | Main Effects1 |
–2 | Two-Way Interactions2 |
–3 | Three-Way Interactions2 |
. | . |
. | . |
. | . |
–n_factors | (n_factors)-way Interactions2 |
–n_factors – 1 | Effects Error Term |
–n_factors – 2 | Residual3 |
–n_factors – 3 | Corrected Total |
Notes: 1. The number of main effects is equal to n_factors + 1 if n_locations > 1, and n_factors if n_locations = 1. The first row of values, anova_table(0,0) through anova_table(0,5) contain the location effect if n_locations > 1. If n_locations = 1, then these values are the effects for factor 1. 2. The number of interaction effects for the nth-way interactions is equal to: 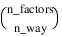 The order of these terms is in ascending order by treatment subscript. The interactions for factor 1 appear first, followed by factor 2, factor 3, and so on. 3. The residual term is only provided when treatments are replicated, i.e., n_levels(n_factors) > 1. | |
note | By default, model_order = n_factors when treatments are replicated, or n_locations > 1. However, if treatments are not replicated and n_locations = 1, model_order = n_factors – 1. |
Output Keywords
N_missing—Number of missing values, if any, found in y. Missing values are denoted with a NaN (Not a Number) value.
Cv—Coefficient of Variation computed by:
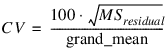
Grand_mean—Mean of all the data across every location.
Factor_means—An array of length n_levels(0) + n_levels(1) + … + n_levels(n_factors–1) containing the factor means.
Factor_std_errors—An n_factors by 2 array containing factor standard errors and their associated degrees of freedom. The first column contains the standard errors for comparing two factor means and the second its associated degrees of freedom.
Two_way_means—One-dimensional array containing the two-way means for all two by two combinations of the factors. If n_factors = 1, this keyword is not valid. The total length of this array when n_factors > 1 is equal to:
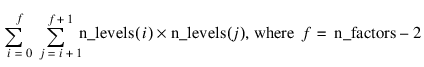
If n_factors > 1, the means would first be produced for all combinations of the first two factors followed by all combinations of the remaining factors using the subscript order suggested by the above formula. For example, if the experiment is a 2x2x2 factorial, the 12 two-way means would appear in the following order: A1B1, A1B2, A2B1, A2B2, A1C1, A1C2, A2C1, A2C2, B1C1, B1C2, B2C1, and B2C2.
Two_way_std_errors—An N_two_way by 2 array containing factor standard errors and their associated degrees of freedom, where:
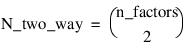
The first column contains the standard errors for comparing two 2-way interaction means and the second its associated degrees of freedom. The ordering of the rows in this array is similar to that used in Two_way_means. For example if n_factors = 4, then N_two_way = 6 with the order AB, AC, AD, BC, BD, CD.
Treatment_means—A 1D array of size:

containing the treatment means. The order of the means is organized in ascending order by the value of the factor identifier. For example, if the experiment is a 2x2x2 factorial, the 8 means would appear in the following order: A1B1C1, A1B1C2, A1B2C1, A1B1C2, A2B1C1, A2B1C2, A2B2C1, and A2B2C2.
Treatment_std_errors—Two element array containing the standard error for comparing treatments based upon the average number of replicates per treatment and its associated degrees of freedom.
Anova_row_labels—An array containing the labels for each of the rows of the returned ANOVA table. The label for the ith row of the ANOVA table can be printed with PRINT, Anova_row_labels(i).
Double—If present and nonzero, double precision is used.
Discussion
The function CRD_FACTORIAL analyzes factorial experiments replicated in different locations. Missing observations are allowed. All factors are regarded as fixed effects in the analysis. However, if multiple locations appear in the data, i.e., n_locations > 1, then all effects involving locations are treated as random effects.
If n_locations = 1, then the residual mean square is used as the error mean square in calculating the F-tests for all other effects. That is:
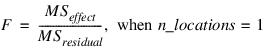
If n_locations > 1 then the error mean squares for all factor F-tests is the pooled location interaction. For example, if n_factors = 2 then the error sum of squares, degrees of freedom and mean squares are calculated by:
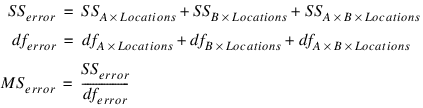
Example
The following example is based upon data from a 3x2x2 completely randomized design conducted at one location. For demonstration purposes, observation 9 is set to missing.
n_obs = 12
n_locations = 1
n_factors = 3
n_levels = [3, 2, 2, 1]
models = TRANSPOSE( $
[ [1, 1, 1, 1], $
[1, 1, 1, 2], $
[1, 1, 2, 1], $
[1, 1, 2, 2], $
[1, 2, 1, 1], $
[1, 2, 1, 2], $
[1, 2, 2, 1], $
[1, 2, 2, 2], $
[1, 3, 1, 1], $
[1, 3, 1, 2], $
[1, 3, 2, 1], $
[1, 3, 2, 2] ])
; Response data
y = [4.42725419998168950, $
2.12795543670654300, $
2.55254390835762020, $
1.21479606628417970, $
2.47588264942169190, $
5.01306104660034180, $
4.73502767086029050, $
4.58392113447189330, $
5.01421167794615030, $
4.11972457170486450, $
6.51671624183654790, $
4.73365202546119690]
a = MACHINE(/Float)
NaN = a.NAN
y(8) = NaN
aov = CRD_FACTORIAL(n_obs, n_locations, n_factors, $
n_levels, models, y, $
N_missing=n_missing, $
Cv=cv, Grand_mean=grand_mean, $
Factor_means=factor_means, $
Factor_std_errors=factor_std_errors, $
Two_way_means=two_way_means, $
Two_way_std_errors=two_way_std_errors, $
Treatment_means=treatment_means, $
Treatment_std_errors=treatment_std_errors, $
Anova_row_labels=anova_row_labels)
; Print Analysis of Variance Table
PRINT, " *** ANALYSIS OF VARIANCE TABLE ***"
PRINT, 'ID', 'DF', 'SSQ', 'MS', 'F-Test', 'p-Value', $
Format='(A12, A6, A8, A8, A8, A9)'
FOR i=0L, (SIZE(aov))(1)-1 DO BEGIN & $
PRINT, anova_row_labels(i), aov(i,0), aov(i,1), $
aov(i,2), aov(i,3), aov(i,4), aov(i,5), Format= $
'(A7, 2X, I3, 3X, F3.0, 2X, F6.2, 2X, F6.2, 2X, ' + $
'F6.2, 4X, F5.3)' & $
ENDFOR
PRINT, ''
PRINT, n_missing, $
Format='("Number of Missing Values Estimated:", I3)'PRINT, grand_mean, $
Format='("Grand Mean :", F7.3)'PRINT, cv, $
Format='("Coefficient of Variation :", F7.3)'PRINT, ''
l = 0 & m = 0
PRINT, "Factor Means"
FOR i=0L, n_factors-1 DO BEGIN & $
PRINT, (i+1), factor_means(m:(m+n_levels(i)-1)), $
Format='(2X, "Factor", I2, ": ", ' + $
STRTRIM(n_levels(i),2) + 'F11.6)' & $
k = FIX(factor_std_errors(l,1)) & $
PRINT, factor_std_errors(i), k, $
Format='(15X, "std. err.(df):", F16.6, "(", I1, ")")' & $l = l + 1 & $
m = m + n_levels(i) & $
ENDFOR
PRINT, ''
l = 0 & m = 0
PRINT, "Two-Way Means"
FOR i=0L, n_factors-1 DO BEGIN & $
FOR j=(i+1), n_factors-1 DO BEGIN & $
PRINT, (i+1), (j+1), Format= $
'(2X, "Factor", I2, " by Factor", I2, ":")' & $
FOR i2=0L, (n_levels(i)-1) DO BEGIN & $
PRINT, two_way_means(m:(m+n_levels(j)-1)) & $
m = m + n_levels(j) & $
ENDFOR & $
k = FIX(two_way_std_errors(l,1)) & $
PRINT, two_way_std_errors(l), k, $
Format='(2X, "std. err.(df): = ", F7.5, ' + $
'"(", I1, ")")' & $l = l + 1 & $
PRINT, '' & $
ENDFOR & $
ENDFOR
PRINT, "Treatment Means"
m = 0
FOR i=0L, n_levels(0)-1 DO $
FOR j=0L, n_levels(1)-1 DO $
FOR k=0L, n_levels(2)-1 DO BEGIN & $
PRINT, (i+1), (j+1), (k+1), treatment_means(m), Format= $
"(2X, 'Treatment[', I1, '][', I1, '][', I1, ']', " + $
"' Mean:', F7.4)" & $
m = m + 1 & $
ENDFOR
PRINT, ''
k = FIX(Treatment_std_errors(1)) & $
PRINT, Treatment_std_errors(0), k, $
Format='("Treatment Std. Err.(df): = ", F7.5, "(", I1, ")")'Output
*** ANALYSIS OF VARIANCE TABLE ***
ID DF SSQ MS F-test P-Value
[1] -1 2. 13.06 6.53 7.84 0.245
[2] -1 1. 0.11 0.11 0.13 0.781
[3] -1 1. 1.30 1.30 1.56 0.429
[1]x[2] -2 2. 3.77 1.88 2.26 0.425
[1]x[3] -2 2. 5.25 2.63 3.15 0.370
[2]x[3] -2 1. 0.56 0.56 0.67 0.563
Error -4 1. 1.67 1.67 NaN NaN
Total -5 10. 25.72 NaN NaN NaN
Number of Missing Values Estimated: 1
Grand Mean : 3.962
Coefficient of Variation : 32.574
Factor Means
Factor 1: 2.580637 4.201973 5.101930
std. err.(df): 0.912459(1)
Factor 2: 3.866917 4.056109
std. err.(df): 0.745020(1)
Factor 3: 4.290842 3.632185
std. err.(df): 0.745020(1)
Two-Way Means
Factor 1 by Factor 2:
3.27760 1.88367
3.74447 4.65947
4.57868 5.62518
std. err.(df): = 1.29041(1)
Factor 1 by Factor 3:
3.48990 1.67138
3.60546 4.79849
5.77717 4.42669
std. err.(df): = 1.29041(1)
Factor 2 by Factor 3:
3.98025 3.75358
4.60143 3.51079
std. err.(df): = 1.05362(1)
Treatment Means
Treatment[1][1][1] Mean: 4.4273
Treatment[1][1][2] Mean: 2.1280
Treatment[1][2][1] Mean: 2.5525
Treatment[1][2][2] Mean: 1.2148
Treatment[2][1][1] Mean: 2.4759
Treatment[2][1][2] Mean: 5.0131
Treatment[2][2][1] Mean: 4.7350
Treatment[2][2][2] Mean: 4.5839
Treatment[3][1][1] Mean: 5.0376
Treatment[3][1][2] Mean: 4.1197
Treatment[3][2][1] Mean: 6.5167
Treatment[3][2][2] Mean: 4.7337
Treatment Std. Err.(df): = 1.82492(1)