ANOVANESTED Function
Analyzes a completely nested random model with possibly unequal numbers in the subgroups.
Usage
result = ANOVANESTED(n_factors, eq_option, n_levels, y)
Input Parameters
n_factors—Number of factors (number of subscripts) in the model, including error.
eq_option—Equal numbers option.
0—Unequal numbers in the subgroups1—Equal numbers in the subgroupsn_levels—One-dimensional array with the number of levels.
If eq_option = 1, n_levels is of length n_factors and contains the number of levels for each of the factors. In this case, the additional variables listed in Table 5-26: Additional Variables are referred to in the description of ANOVANESTED:
Variable | Description |
|---|---|
LNL | n_levels(1) + ... + n_levels(0) * n_levels(1) * ... * n_levels(n_factors – 2) |
LNLNF | n_levels(0) * n_levels(1) * ...* n_levels(n_factors – 2) |
NOBS | The number of observations. NOBS equals n_levels(0) * n_levels(1) * ... * n_levels(n_factors-1) |
If eq_option = 0, n_levels contains the number of levels of each factor at each level of the factor in which it is nested. In this case, the following additional variables are referred to in the description of ANOVANESTED:
LNL—Length of n_levels.LNLNF—Length of the subvector of n_levels for the last factor.NOBS—Number of observations. NOBS equals the sum of the last LNLNF elements of n_levels. n_levels(n_factors-1).For example, a random one-way model with two groups, five responses in the first group and ten in the second group, would have LNL = 3, LNLNF = 2, NOBS = 15, n_levels(0) = 2, n_levels(1) = 5, and n_levels(2) = 10.
y—One-dimensional array of length NOBS containing the responses.
Returned Value
result—The p-value for the F-statistic.
Input Keywords
Double—If present and nonzero, then double precision is used.
Confidence—Confidence level for two-sided interval estimates on the variance components, in percent. Confidence percent confidence intervals are computed, hence, Confidence must be in the interval [0.0, 100.0). Confidence often will be 90.0, 95.0, or 99.0. For one-sided intervals with confidence level ONECL, ONECL in the interval [50.0, 100.0), set Confidence = 100.0 – 2.0 * (100.0 - ONECL). Default: Confidence = 95.0
Output Keywords
Anova_Table—Named variable which stores the size 15 array containing the analysis of variance table. Analysis of variance statistics are as follows:
0—Degrees of freedom for the model1—Degrees of freedom for error2—Total (corrected) degrees of freedom3—Sum of squares for the model4—Sum of squares for error5—Total (corrected) sum of squares6—Model mean square7—Error mean square8—Overall F-statistic9—p-value10—R2 (in percent)11—Adjusted R2 (in percent)12—Estimate of the standard deviation13—Overall mean of y14—Coefficient of variation (in percent)Var_Comp—Named variable into which an array of size n_factors by 9 containing statistics relating to the particular variance components in the model is stored. Rows of Var_Comp correspond to the n_factors factors. Columns of Var_Comp are as follows:
1—Degrees of freedom2—Sum of squares3—Mean squares4—F-statistic5—p-value for F test6—Variance component estimate7—Percent of variance explained by variance component8—Lower endpoint for confidence interval on the variance component9—Upper endpoint for confidence interval on the variance componentIf a test for error variance equal to zero cannot be performed, Var_Comp(n_factors, 4) and Var_Comp(n_factors, 5) are set to NaN.
Ems—One-dimensional array of length n_factors * (n_factors + 1)/2 with expected mean square coefficients.
Y_Means—One-dimensional array containing the subgroup means.
eq_option | Length of y means |
|---|---|
0 | 1 + n_levels(0) + n_levels(1) + ... n_levels((LNL - LNLNF)-1) (See description of argument n_levels for definitions of LNL and LNLNF.) |
1 | 1 + n_levels(0) + n_levels(0) * n_levels(1) + ... + n_levels(0)* n_levels(1) * ... * n_levels (n_factors – 2) |
If the factors are labeled A, B, C, and error, the ordering of the means is grand mean, A means, AB means, and then ABC means.
Discussion
Function ANOVANESTED analyzes a nested random model with equal or unequal numbers in the subgroups. The analysis includes an analysis of variance table and computation of subgroup means and variance component estimates. Anderson and Bancroft (1952, pages 325−330) discuss the methodology. The analysis of variance method is used for estimating the variance components. This method solves a linear system in which the mean squares are set to the expected mean squares. A problem that Hocking (1985, pages 324−330) discusses is that this method can yield negative variance component estimates. Hocking suggests a diagnostic procedure for locating the cause of a negative estimate. It may be necessary to reexamine the assumptions of the model.
Example 1
An analysis of a three-factor nested random model with equal numbers in the subgroups is performed using data discussed by Snedecor and Cochran (1967, Table 10.16.1, pages 285−288). The responses are calcium concentrations (in percent, dry basis) as measured in the leaves of turnip greens. Four plants are taken at random, then three leaves are randomly selected from each plant. Finally, from each selected leaf two samples are taken to determine calcium concentration. The model is:
yijk = μ + αi + βij + eijk i = 1, 2, 3, 4; j = 1, 2, 3; k = 1, 2
where yijk is the calcium concentration for the kth sample of the jth leaf of the ith plant, the αi’s are the plant effects and are taken to be independently distributed:
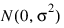
the βij’s are leaf effects each independently distributed:
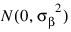
and the εijk’s are errors each independently distributed N(0, σ2). The effects are all assumed to be independently distributed. The data is given in Table 5-28: Calcium Concentrations:
Plant | Leaf | Samples | |
|---|---|---|---|
1 | 1 2 3 | 3.28 3.52 2.88 | 3.09 3.48 2.80 |
2 | 1 2 3 | 2.46 1.87 2.19 | 2.44 1.92 2.19 |
3 | 1 2 3 | 2.77 3.74 2.55 | 2.66 3.44 2.55 |
4 | 1 2 3 | 3.78 4.07 3.31 | 3.87 4.12 3.31 |
PRO print_results, p, at, ems, y_means, var_comp
anova_labels = ['degrees of freedom for model', $
'degrees of freedom for error', $
'total (corrected) degrees of freedom', $
'sum of squares for model', 'sum of squares for error', $
'total (corrected) sum of squares', 'model mean square', $
'error mean square', 'F-statistic', 'p-value', $
'R-squared (in percent)', $
'adjusted R-squared (in percent)', $
'est. standard deviation of within error', $
'overall mean of y', $
'coefficient of variation (in percent)']
ems_labels = ['Effect A and Error', 'Effect A and Effect B', $
'Effect A and Effect A', 'Effect B and Error', $
'Effect B and Effect B', 'Error and Error']
components_labels = ['degrees of freedom for A', $
'sum of squares for A', 'mean square of A', $
'F-statistic for A', 'p-value for A', $
'Estimate of A', 'Percent Variation Explained by A', $
'95% Confidence Interval Lower Limit for A', $
'95% Confidence Interval Upper Limit for A', $
'degrees of freedom for B', 'sum of squares for B', $
'mean square of B', 'F-statistic for B', 'p-value for B', $
'Estimate of B', 'Percent Variation Explained by B', $
'95% Confidence Interval Lower Limit for B', $
'95% Confidence Interval Upper Limit for B', $
'degrees of freedom for Error', $
'sum of squares for Error', 'mean square of Error', $
'F-statistic for Error', 'p-value for Error', $
'Estimate of Error', 'Percent Explained by Error', $
'95% Confidence Interval Lower Limit for Error', $
'95% Confidence Interval Upper Limit for Error']
means_labels = ['Grand mean', $
' A means 1', $
' A means 2', $
' A means 3', $
' A means 4', $
'AB means 1 1', $
'AB means 1 2', $
'AB means 1 3', $
'AB means 2 1', $
'AB means 2 2', $
'AB means 2 3', $
'AB means 3 1', $
'AB means 3 2', $
'AB means 3 3', $
'AB means 4 1', $
'AB means 4 2', $
'AB means 4 3']
PRINT, 'p value of F statistic =', p
PRINT, ' * * * Analysis of Variance * * *'
FOR i=0L, 14 DO $
PM, anova_labels(i), at(i), Format = '(A40, F20.5)'
PRINT, ' * * * Expected Mean Square Coefficients * * *'
FOR i=0L, 5 DO $
PM, ems_labels(i), ems(i), Format = '(A40, F20.2)'
PRINT, ' * * Analysis of Variance / Variance Components * *'
k = 0
FOR i=0L, 2 DO BEGIN
FOR j=0L, 8 DO BEGIN
PM, components_labels(k), var_comp(i, j), $
Format = '(A45, F20.5)'
k = k + 1
ENDFOR
ENDFOR
PRINT, 'means', Format = '(A20)'
FOR i=0L, 16 DO $
PM, means_labels(i), y_means(i), Format ='(A20, F20.2)'
END
y = [3.28, 3.09, 3.52, 3.48, 2.88, 2.80, 2.46, 2.44, 1.87, $
1.92, 2.19, 2.19, 2.77, 2.66, 3.74, 3.44, 2.55, 2.55, $
3.78, 3.87, 4.07, 4.12, 3.31, 3.31]
n_levels = [4, 3, 2]
p = ANOVANESTED(3, 1, n_levels, y, Anova_Table = at, Ems=ems, $
Y_Means = y_means, Var_Comp = var_comp)
print_results, p, at, ems, y_means, var_comp
This results in the following output:
p value of F statistic = 0.00000
* * * Analysis of Variance * * *
degrees of freedom for model 11.00000
degrees of freedom for error 12.00000
total (corrected) degrees of freedom 23.00000
sum of squares for model 10.19054
sum of squares for error 0.07985
total (corrected) sum of squares 10.27040
model mean square 0.92641
error mean square 0.00665
F-statistic 139.21599
p-value 0.00000
R-squared (in percent) 99.22248
adjusted R-squared (in percent) 98.50976
est. standard deviation of within error 0.08158
overall mean of y 3.01208
coefficient of variation (in percent) 2.70826
* * * Expected Mean Square Coefficients * * *
Effect A and Error 1.00
Effect A and Effect B 2.00
Effect A and Effect A 6.00
Effect B and Error 1.00
Effect B and Effect B 2.00
Error and Error 1.00
* * Analysis of Variance / Variance Components * *
degrees of freedom for A 3.00000
sum of squares for A 7.56034
mean square of A 2.52011
F-statistic for A 7.66516
p-value for A 0.00973
Estimate of A 0.36522
cent Variation Explained by A 68.53015
95% Confidence Interval Lower Limit for A 0.03955
95% Confidence Interval Upper Limit for A 5.78674
degrees of freedom for B 8.00000
sum of squares for B 2.63020
mean square of B 0.32878
F-statistic for B 49.40642
p-value for B 0.00000
Estimate of B 0.16106
Percent Variation Explained by B 30.22121
95% Confidence Interval Lower Limit for B 0.06967
95% Confidence Interval Upper Limit for B 0.60042
degrees of freedom for Error 12.00000
sum of squares for Error 0.07985
mean square of Error 0.00665
F-statistic for Error NaN
p-value for Error NaN
Estimate of Error 0.00665
Percent Explained by Error 1.24864
95% Confidence Interval Lower Limit for Error 0.00342
95% Confidence Interval Upper Limit for Error 0.01813
means
Grand mean 3.01
A means 1 3.17
A means 2 2.18
A means 3 2.95
A means 4 3.74
AB means 1 1 3.18
AB means 1 2 3.50
AB means 1 3 2.84
AB means 2 1 2.45
AB means 2 2 1.89
AB means 2 3 2.19
AB means 3 1 2.72
AB means 3 2 3.59
AB means 3 3 2.55
AB means 4 1 3.82
AB means 4 2 4.10
AB means 4 3 3.31
