ANOVA1 Function
Analyzes a one-way classification model.
Usage
result = ANOVA1(n, y)
Input Parameters
n—One-dimensional array containing the number of responses for each group.
y—One-dimensional array of length:
n(0) + n(1) + ...+ n(N_ELEMENTS(n) – 1)
containing the responses for each group.
Returned Value
result—The p-value for the F-statistic.
Input Keywords
Double—If present and nonzero, then double precision is used.
Confidence—Confidence level for the simultaneous interval estimation. If Tukey is specified, Confidence must be in the range [90.0, 99.0); otherwise, Confidence is in the range [0.0, 100.0). Default: Confidence = 95.0
Output Keywords
Anova_Table—Named variable into which the analysis of variance table is stored. The analysis of variance statistics are as follows:
0—degrees of freedom for the model1—degrees of freedom for error2—total (corrected) degrees of freedom3—sum of squares for the model4—sum of squares for error5—total (corrected) sum of squares6—model mean square7—error mean square8—overall F-statistic9—p-value10—R2 (in percent)11—Adjusted R2 (in percent)12—estimate of the standard deviation13—overall mean of y14—coefficient of variation (in percent)Group_Means—Named variable into which the array containing the group means is stored.
Group_Std_Dev—Named variable into which the array containing the group standard deviations is stored.
Group_Counts—Named variable into which the array containing the number of nonmissing observations for the groups is stored.
Tukey, Dunn_Sidak, Bonferroni, Scheffe, One_At_A_Time—Named variable into which the array containing the statistics relating to the difference of means is stored. On return, the named variable contains an array of size:
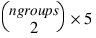
where ngroups = N_ELEMENTS (n).
0—group number for the ith mean1—group number for the jth mean2—difference of means (ith mean) − (jth mean)3—lower confidence limit for the difference4—upper confidence limit for the differenceFunction ANOVA1 computes confidence intervals on all pairwise differences of means using one of six methods: Tukey, Tukey-Kramer, Dunn-Sidák, Bonferroni, Scheffé, or Fisher’s LSD (One-at-a-Time). If Tukey is specified, Tukey confidence intervals are calculated if the group sizes are equal; otherwise, the Tukey-Kramer confidence intervals are calculated.
Discussion
Function ANOVA1 performs an analysis of variance of responses from a one-way classification design. The model is:
yij = μi + εij i = 1, 2, ..., k; j = 1, 2, ..., ni
where the observed value yij constitutes the jth response in the ith group, μi denotes the population mean for the ith group, and the εij arguments are errors that are identically and independently distributed normal with mean 0 and variance σ2. Function ANOVA1 requires the yij observed responses as input into a single vector y with responses in each group occupying contiguous locations. The analysis of variance table is computed along with the group sample means and standard deviations. A discussion of formulas and interpretations for the one-way analysis of variance problem appears in most statistics texts, e.g., Snedecor and Cochran (1967, Chapter 10).
Function ANOVA1 computes simultaneous confidence intervals on all:
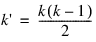
pairwise comparisons of k means μ1, μ2, ..., μk in the one-way analysis of variance model. Any of several methods can be chosen. A good review of these methods is given by Stoline (1981). The methods also are discussed in many statistics texts, e.g., Kirk (1982, pp. 114–127).
Let s2 be the estimated variance of a single observation. Let ν be the degrees of freedom associated with s2. Let:
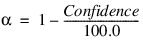
The methods are summarized as follows:
Tukey method: The Tukey method gives the narrowest simultaneous confidence intervals for all pairwise differences of means μi – μj in balanced (n1 = n2 = ... nk = n) one-way designs. The method is exact and uses the Studentized range distribution. The formula for the difference μi – μj is given by the following:
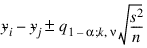
where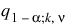 
is the (1 – α ) 100 percentage point of the Studentized range distribution with parameters k and ν.
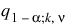is the (1 – α ) 100 percentage point of the Studentized range distribution with parameters k and ν.Tukey-Kramer method: The Tukey-Kramer method is an approximate extension of the Tukey method for the unbalanced case. (The method simplifies to the Tukey method for the balanced case.) The method always produces confidence intervals narrower than the Dunn-Sidak and Bonferroni methods. Hayter (1984) proved that the method is conservative, i.e., the method guarantees a confidence coverage of at least (1 – α) 100. Hayter’s proof gave further support to earlier recommendations for its use (Stoline 1981). (Methods that are currently better are restricted to special cases and only offer improvement in severely unbalanced cases; see, for example, Spurrier and Isham 1985.) The formula for the difference μi – μj is given by the following:
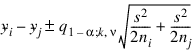
Dunn-Sidák method: The Dunn-Sidak method is a conservative method. The method gives wider intervals than the Tukey-Kramer method. (For large ν and small α and k, the difference is only slight.) The method is slightly better than the Bonferroni method and is based on an improved Bonferroni (multiplicative) inequality (Miller 1980, pp. 101, 254–255). The method uses the t distribution (see function TCDF. The formula for the difference μi – μj is given by the following:
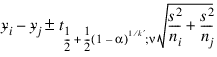
where tf;v is the 100f percentage point of the t distribution with ν degrees of freedom.
Bonferroni method: The Bonferroni method is a conservative method based on the Bonferroni (additive) inequality (Miller, p. 8). The method uses the t distribution. The formula for the difference μi – μj is given by the following:
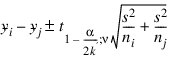
Scheffé method: The Scheffé method is an overly conservative method for simultaneous confidence intervals on pairwise difference of means. The method is applicable for simultaneous confidence intervals on all contrasts, i.e., all linear combinations:
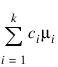
where the following is true:
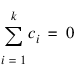
This method can be recommended here only if a large number of confidence intervals on contrasts, in addition to the pairwise differences of means, are to be constructed. The method uses the F distribution (see function FCDF. The formula for the difference μi – μj is given by the following:
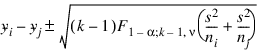
where:
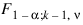
is the (1 – α) 100 percentage point of the F distribution with k – 1 and ν degrees of freedom.
One-at-a-Time t method (Fisher’s LSD): The One-at-a-Time t method is appropriate for constructing a single confidence interval. The confidence percentage input is appropriate for one interval at a time. The method has been used widely in conjunction with the overall test of the null hypothesis μ1 = μ2 = ... = μk by the use of the F statistic. Fisher’s LSD (least significant difference) test is a two-stage test that proceeds to make pairwise comparisons of means only if the overall F test is significant. Milliken and Johnson (1984, p. 31) recommend LSD comparisons after a significant F only if the number of comparisons is small and the comparisons were planned prior to the analysis. If many unplanned comparisons are made, they recommend Scheffé’s method. If the F test is insignificant, a few planned comparisons for differences in means can still be performed by using either Tukey, Tukey-Kramer, Dunn-Sidak or Bonferroni methods. Because the F test is insignificant, Scheffé’s method does not yield any significant differences. The formula for the difference μi – μj is given by the following:
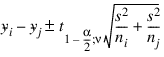
Example 1
This example computes a one-way analysis of variance for data discussed by Searle (1971, Table 5.1, pp. 165–179). The responses are plant weights for six plants of three different types shown in Table 5-16: Plant Types—three normal, two off-types, and one aberrant.
Normal | Off-Type | Aberrant |
|---|---|---|
101 | 84 | 32 |
105 | 88 | |
94 |
n = [3,2,1]
y = [101.0, 105.0, 94.0, 84.0, 88.0, 32.0]
PRINT,'p-value = ', ANOVA1(n, y)
; PV-WAVE prints: p-value = 0.00276887
Example 2: Multiple Comparisons
Simultaneous confidence intervals are generated for the measurements of cold-cranking power for five models of automobile batteries shown in Table 5-17: Cold-Cranking Power for Batteries. Nelson (1989, pp. 232–241) provided the data and approach.
Model 1 | Model 2 | Model 3 | Model 4 | Model 5 |
|---|---|---|---|---|
41 | 42 | 27 | 48 | 28 |
43 | 43 | 26 | 45 | 32 |
42 | 46 | 28 | 51 | 37 |
46 | 38 | 27 | 46 | 25 |
The Tukey method is chosen for the analysis of pairwise comparisons, with a confidence level of 99 percent. The means and their confidence limits are output. First, a procedure to print out the results is defined.
n = [3,2,1]
y = [101.0, 105.0, 94.0, 84.0, 88.0, 32.0]
PRINT,'p-value = ', ANOVA1(n, y)
; PV-WAVE prints: p-value = 0.00276887
This results in the following output:
* *Analysis of Variance * *
df for among groups 4.00
df for within groups 15.00
total (corrected) df 19.00
ss for among groups 1242.20
ss for within groups 150.75
total (corrected) ss 1392.95
mean square among groups 310.55
mean square within groups 10.05
F-statistic 30.90
P-value 0.00
R-squared (in percent) 89.18
adjusted R-squared (in percent) 86.29
est. std of within group error 3.17
overall mean of y 38.05
coef. of variation (in percent) 8.33
* *Differences of Means * *
groups difference lower limit upper limit
1 2 0.75 -8.05 9.55
1 3 16.00 7.20 24.80
1 4 -4.50 -13.30 4.30
1 5 12.50 3.70 21.30
2 3 15.25 6.45 24.05
2 4 -5.25 -14.05 3.55
2 5 11.75 2.95 20.55
3 4 -20.50 -29.30 -11.70
3 5 -3.50 -12.30 5.30
4 5 17.00 8.20 25.80
