SCAT2DINTERP Function
Computes a smooth bivariate interpolant to scattered data that is locally a quintic polynomial in two variables.
Usage
result = SCAT2DINTERP(xydata, fdata, xout, yout)
Input Parameters
xydata—Two-dimensional array containing the data points for the interpolation problem. Argument xydata is dimensioned (2, N_ELEMENTS (fdata)). The ith data point (xi, yi) is stored in xydata (0, i) = xi and xydata (1, i) = yi.
fdata—One-dimensional array containing the values to be interpolated.
xout—One-dimensional array specifying the x values for the output grid. It must be strictly increasing.
yout—One-dimensional array specifying the y values for the output grid. It must be strictly increasing.
Returned Value
result—A two-dimensional array containing the grid of values of the interpolant.
Input Keywords
Double—If present and nonzero, double precision is used.
Discussion
SCAT2DINTERP computes a C1 interpolant to scattered data in the plane. Given the data points (in R3):
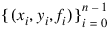
where n = N_ELEMENTS(xydata) / 2, SCAT2DINTERP returns the values of the interpolant s on the user-specified grid. The computation of s is as follows.
First, the Delaunay triangulation of the points:
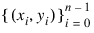
is computed. On each triangle T in this triangulation, s has the following form:
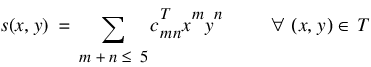
Thus, s is a bivariate quintic polynomial on each triangle of the triangulation. In addition:
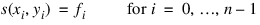
and s is continuously differentiable across the boundaries of neighboring triangles. These conditions do not exhaust the freedom implied by the above representation. This additional freedom is exploited in an attempt to produce an interpolant that is faithful to the global shape properties implied by the data. For more information on this procedure, refer to the article by Akima (1978). The output grid is specified by the two real vectors, xout and yout, that represent the first (second) coordinates of the grid.
Example
In this example, SCAT2DINTERP is used to fit a surface to randomly scattered data. The resulting surface and the original data points are then plotted as shown in Figure 4-16: Fit to Scattered Data.
RANDOMOPT, Set = 12345
ndata = 15
xydata = FLTARR(2, ndata)
xydata(*) = RANDOM(2 * ndata)
fdata = RANDOM(ndata)
x = xydata(0, *)
y = xydata(1, *)
; Define the grid used to evaluate the computed surface.
ngrid = 20
xout = FINDGEN(ngrid)/(ngrid - 1)
yout = FINDGEN(ngrid)/(ngrid - 1)
; Call SCAT2DINTERP.
surf = SCAT2DINTERP(xydata, fdata, xout, yout)
; Plot the computed surface.
SURFACE, surf, xout, yout, /Save, Ax = 45, Charsize = 1.5
; Plot the original data points.
PLOTS, x, y, fdata, /T3d, Symsize = 2, Psym = 2
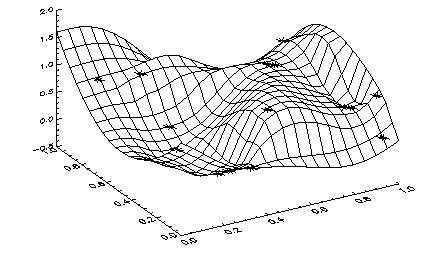 |
Fatal Errors
MATH_DUPLICATE_XYDATA_VALUES—Two-dimensional data values must be distinct.
MATH_XOUT_NOT_STRICTLY_INCRSING—Vector xout must be strictly increasing.
MATH_YOUT_NOT_STRICTLY_INCRSING—Vector yout must be strictly increasing.





