Computes a smooth cubic spline approximation to noisy data by using cross-validation to estimate the smoothing parameter or by directly choosing the smoothing parameter.

xdata—One-dimensional array containing the abscissas of the problem.

fdata—One-dimensional array containing the ordinates of the problem.

result—The structure that represents the cubic spline.

Double—If present and nonzero, double precision is used.

Weights—Array containing the weights to be used in the problem. Default: all weights are equal to 1

Smpar—Specifies the real, scalar smoothing parameter explicitly. See Discussion below for more details.

Function CSSMOOTH is designed to produce a C2 cubic spline approximation to a data set in which the function values are noisy. This spline is called a smoothing spline.

Consider first the situation when the optional keyword Smpar is selected. Then, a natural cubic spline with knots at all the data abscissas x = xdata is computed, but it does not interpolate the data (xi, fi). The smoothing spline s is the unique C2 function which minimizes:

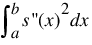
subject to the constraint:

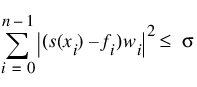
where w = Weights, σ = Smpar is the smoothing parameter, and n = N_ELEMENTS(xdata).

Recommended values for σ depend on the weights w. If an estimate for the standard deviation of the error in the value fi is available, then wi should be set to the inverse of this value. The smoothing parameter σ should be chosen in the confidence interval corresponding to the left side of the above inequality; that is:

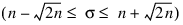
Function CSSMOOTH is based on an algorithm of Reinsch (1967). This algorithm also is discussed in de Boor (1978, pp. 235–243).

The default for this function chooses the smoothing parameter σ by a statistical technique called cross-validation. For more information on this topic, refer to Craven and Wahba (1979).

The return value for this function is a structure containing all the information to determine the spline (stored as a piecewise polynomial) that is computed by this procedure.

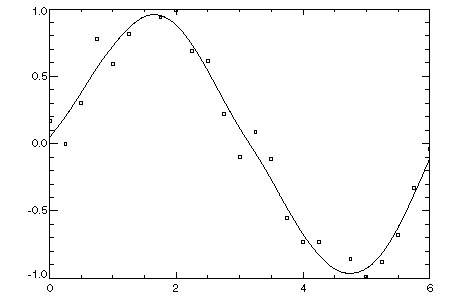
In this example, function values are contaminated by adding a small “random” amount to the correct values. Function CSSMOOTH is used to approximate the original, uncontaminated data as shown in Figure 4-14: Smoothing Spline.

; Generate the data.

n = 25

x = 6 * FINDGEN(n)/(n - 1)

f = SIN(x) + .5 * (RANDOM(n) - .5)

; Compute the fit.

pp = CSSMOOTH(x, f)

; Evaluate the computed fit at 100 values in [0, 6].

x2 = 6 * FINDGEN(100)/99

ppeval = SPVALUE(x2, pp)

; Plot the results.

PLOT, x2, ppeval

OPLOT, x, f, Psym = 6, Symsize = .5

MATH_MAX_ITERATIONS_REACHED—Maximum number of iterations has been reached. The best approximation is returned.

MATH_DUPLICATE_XDATA_VALUES—The xdata values must be distinct.

MATH_NEGATIVE_WEIGHTS—All weights must be greater than or equal to zero.