CSSHAPE Function
Computes a shape-preserving cubic spline.
Usage
result = CSSHAPE(xdata, fdata)
Input Parameters
xdata—One-dimensional array containing the abscissas of the interpolation problem.
fdata—One-dimensional array containing the ordinates for the interpolation problem.
Returned Value
result—A structure that represents the cubic spline interpolant.
Input Keywords
Double—If present and nonzero, double precision is used.
Concave—If present and nonzero, CSSHAPE produces a cubic interpolant that preserves the concavity of the data.
Itmax—Allows the user to set the maximum number of iterations of Newton’s Method. To use Itmax, keyword Concave must also be set. Default: Itmax = 25
Discussion
Function CSSHAPE computes a C1 cubic spline interpolant to a set of data points (xi, fi) for the following:
i = 0, ..., (N_ELEMENTS(xdata) – 1) = (n – 1)
The breakpoints of the spline are the abscissas. This computation is based on a method by Akima (1970) to combat wiggles in the interpolant. Endpoint conditions are automatically determined by the program (see Akima 1970, de Boor 1978).
If the Concave keyword is set, then this function computes a cubic spline interpolant to the data. For ease of explanation, xi < xi + 1 is assumed, although it is not necessary for the user to sort these data values. If the data are strictly convex, then the computed spline is convex, C2, and minimizes the expression
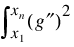
over all convex C1 functions that interpolate the data. In the general case, when the data have both convex and concave regions, the convexity of the spline is consistent with the data, and the above integral is minimized under the appropriate constraints. For more information on this interpolation scheme, refer to Micchelli et al. (1985) and Irvine et al. (1986).
One important feature of the splines produced by this function is that it is not possible, a priori, to predict the number of breakpoints of the resulting interpolant. In most cases, there will be breakpoints at places other than data locations. This function should be used when it is important to preserve the convex and concave regions implied by the data.
Both methods are nonlinear, and although the interpolant is a piecewise cubic, cubic polynomials are not reproduced. (However, linear polynomials are reproduced.) This explains the theoretical error estimate below.
If the data points arise from the values of a smooth (for example, C4) function f, i.e., fi = f(xi), then the error behaves in a predictable fashion. Let ξ be the breakpoint vector for either of the above spline interpolants. Then, the maximum absolute error satisfies:
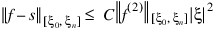
where:
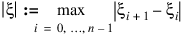
and ξm is the last breakpoint.
The returned value for this function is a structure. This structure contains all the information to determine the spline (stored as a piecewise polynomial) that is computed by this function. For example, the following code sequence evaluates this spline at x and returns the value in y:
y = SPVALUE(x, spline)
Example 1
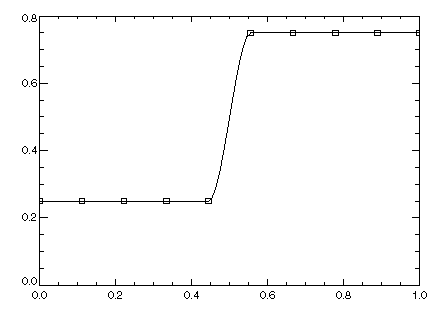
In this example, a cubic spline interpolant to function values is computed. Evaluations of the computed spline are plotted along with the original data values.
; Define the abscissas.
x = FINDGEN(10)/9
; Define the function values.
f = FLTARR(10)
f(0:4) = 0.25
f(5:9) = 0.75
; Compute the interpolant.
pp = CSSHAPE(x, f)
; Evaluate the interpolant at 100 values in [0,1].
ppval = SPVALUE(FINDGEN(100)/99, pp)
; Plot the results.
PLOT, FINDGEN(100)/99, ppval
OPLOT, x, f, Psym = 6
 |
Example 2
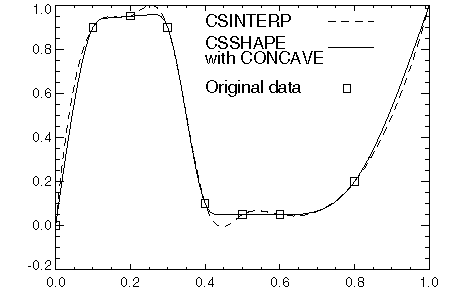
This example compares interpolants computed by CSINTERP and CSSHAPE with keyword Concave, as shown in Figure 4-4: Cubic Spline Comparison.
; Define the data set and compute interpolant from CSINTERP.
x = [0, .1, .2, .3, .4, .5, .6, .8, 1]
y = [0, .9, .95, .9, .1, .05, .05, .2, 1]
pp1 = CSINTERP(x, y)
; Compute the interpolant from CSSHAPE with keyword Concave.
pp2 = CSSHAPE(x, y, /Concave)
x2 = FINDGEN(100)/99
PLOT, x2, SPVALUE(x2, pp1), Linestyle = 2
OPLOT, x2, SPVALUE(x2, pp2)
OPLOT, x, y, Psym = 6
XYOUTS, .4, .9, 'CSINTERP', Charsize = 1.2
OPLOT, [.73, .85], [.925, .925], Linestyle = 2
XYOUTS, .4, .8, 'CSSHAPE !cwith CONCAVE', Charsize = 1.2
OPLOT, [.73, .85], [.8, .8]
XYOUTS, .4, .6, 'Original data', Charsize = 1.2
OPLOT, [.73], [.622], Psym = 6
 |
Warning Errors
MATH_MAX_ITERATIONS_REACHED—Maximum number of iterations has been reached. The best approximation is returned.
Fatal Errors
MATH_DUPLICATE_XDATA_VALUES—The xdata values must be distinct.





