RANKS Function
Computes the ranks, normal scores, or exponential scores for a vector of observations.
Usage
result = RANKS(x)
Input Parameters
x—One-dimensional array containing the observations to be ranked.
Returned Value
result—A one-dimensional array containing the rank (or optionally, a transformation of the rank) of each observation.
Input Keywords
Double—If present and nonzero, double precision is used.
Average_Tie, Highest, Lowest, Random_Split—At most, one of these keywords can be set to a nonzero value to change the method used to assign a score to tied observations.
Average_Tie—average of the scores of the tied observations (default).Highest—highest score in the group of ties.Lowest—lowest score in the group of ties.Random_Split—tied observations are randomly split using a random-number generator.Fuzz—Value used to determine when two items are tied. If
ABS(x(I) – x(J)) is less than or equal to Fuzz, then x(I) and x(J) are said to be tied. Default: Fuzz = 0.0
ABS(x(I) – x(J)) is less than or equal to Fuzz, then x(I) and x(J) are said to be tied. Default: Fuzz = 0.0
Ranks, Blom_Scores, Tukey_Scores, Vdw_Scores, Exp_Norm_Scores, Savage_Scores—At most, one of these keywords can be set to a nonzero value to specify the type of values returned.
Ranks—ranks (default)Blom_Scores—Blom version of normal scoresTukey_Scores—Tukey version of normal scoresVdw_Scores—Van der Waerden version of normal scoresExp_Norm_Scores—expected value of normal order statistics (for tied observations, the average of the expected normal scores)Savage_Scores—Savage scores (expected value of exponential order statistics)Discussion
Ties
If the assignment RANK = RANKS(x) is made, then in data without ties, the output values are the ordinary ranks (or a transformation of the ranks) of the data in x. If x(i) has the smallest value among the values in x and there is no other element in x with this value, then RANK(i) = 1. If both x(i) and x(j) have the same smallest value, then the output value depends on the option used to break ties. Table 2-3: Tie Results shows the results for some of the keywords.
Keyword | Result |
|---|---|
Average_Tie | result ( i ) = result ( j ) = 1.5 |
Highest | result ( i ) = result ( j ) = 2.0 |
Lowest | result ( i ) = result ( j ) = 1.0 |
Random_Split | result ( i ) = 1.0 and result ( j ) = 2.0 or, randomly, result ( i ) = 2.0 and result ( j ) = 1.0 |
When the ties are resolved randomly, function RANDOM is used to generate random numbers. Different results occur from different executions of the program unless the “seed” of the random-number generator is set explicitly by use of the function RANDOMOPT ( ).
Scores
Normal and other functions of the ranks can optionally be returned. Normal scores can be defined as the expected values, or approximations to the expected values, of order statistics from a normal distribution. The simplest approximations are obtained by evaluating the inverse cumulative normal distribution function, NORMALCDF (with keyword Inverse), at the ranks scaled into the open interval (0,1).
In the Blom version (Blom 1958), the scaling transformation for the rank ri (1 ≤ ri ≤ n, where n is the sample size) is (ri – 3/8) / (n + 1/4). The Blom normal score corresponding to the observation with rank ri is:
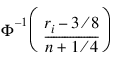
where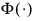 
is the normal cumulative distribution function.
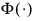is the normal cumulative distribution function.Adjustments for ties are made after the normal score transformation; that is, if x(i) equals x(j) (within Fuzz) and their value is the kth smallest in the data set, the Blom normal scores are determined for ranks of k and k + 1. Then, these normal scores are averaged or selected in the manner specified. (Whether the transformations are made first or the ties are resolved first is irrelevant, except when Average_Tie is specified.)
In the Tukey version (Tukey 1962), the scaling transformation for the rank ri is (ri – 1/3) / (n + 1/3). The Tukey normal score corresponding to the observation with rank ri follows:
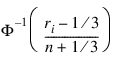
Ties are handled in the same way as for the Blom normal scores.
In the Van der Waerden version (see Lehmann 1975, p. 97), the scaling transformation for the rank ri is ri /(n + 1). The Van der Waerden normal score corresponding to the observation with rank ri is as follows:
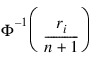
Ties are handled in the same way as for the Blom normal scores.
When option Exp_Norm_Scores is nonzero, the output values are the expected values of the normal order statistics from a sample of size n = N_ELEMNTS(x). If the value in x(i) is the kth smallest, then the value output in RANK (i) is E(zk), where E(·) is the expectation operator, and zk is the kth order statistic in a sample of size n from a standard normal distribution. Ties are handled in the same way as for the Blom normal scores.
Savage scores are the expected values of the exponential order statistics from a sample of size n. These values are called Savage scores because of their use in a test discussed by Savage (1956) and Lehmann (1975). If the value in x(i) is the kth smallest, then the value output in RANK (i) is E(yk) where yk is the kth order statistic in a sample of size n from a standard exponential distribution. The expected value of the kth order statistic from an exponential sample of size n follows:
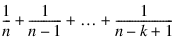
Ties are handled in the same way as for the Blom normal scores.
Example
The data for this example, from Hinkley (1977), contains 30 observations. Note that the fourth and sixth observations are tied, and the third and twentieth observations are tied.
x = [0.77, 1.74, 0.81, 1.20, 1.95, 1.20, 0.47,$
1.43, 3.37, 2.20, 3.00, 3.09, 1.51, 2.10,$
0.52, 1.62, 1.31, 0.32, 0.59, 0.81, 2.81,$
1.87, 1.18, 1.35, 4.75, 2.48, 0.96, 1.89, 0.90, 2.05]
; Call RANKS.
r = RANKS(x)
FOR i=0L, 29 DO PM, i + 1, r(i), Format = '(i5, f7.1)'
This results in the following output:
1 5.0
2 18.0
3 6.5
4 11.5
5 21.0
6 11.5
7 2.0
8 15.0
9 29.0
10 24.0
11 27.0
12 28.0
13 16.0
14 23.0
15 3.0
16 17.0
17 13.0
18 1.0
19 4.0
20 6.5
21 26.0
22 19.0
23 10.0
24 14.0
25 30.0
26 25.0
27 9.0
28 20.0
29 8.0
30 22.0
