MLFF_NETWORK_TRAINER Function

PV-WAVE Advantage > IMSL Statistics Reference Guide > Data Mining > MLFF_NETWORK_TRAINER Function

Trains a multilayered feedforward neural network.

Usage

result = MLFF_NETWORK_TRAINER (network, categorical, continuous, output)

Input Parameters

network—A structure containing the feedforward network. See the MLFF_NETWORK Function. On return, the weights and bias values are updated.

categorical—Array of size n_patterns by n_nominal containing values for the nominal input attributes, where n_patterns is the number of network training patterns, and n_nominal is the number of nominal attributes. The ith row contains the nominal input attributes for the ith training pattern..

continuous—Array of size n_patterns by n_continuous containing values for the continuous input attributes, where n_continuous is the number of continuous attributes. The ith row contains the continuous input attributes for the ith training pattern.

output—Array of size n_patterns by n_outputs containing the output training patterns, where n_outputs is the number of output perceptrons in the network. n_outputs = network.n_outputs. For more details, see the MLFF_NETWORK Function.

Returned Value

result—Array of length 5 containing the summary statistics from the network training, organized as follows:

result(0) = Error sum of squares at the optimum.

result(1) = Total number of Stage I iterations.

result(2) = Smallest error sum of squares after Stage I training.

result(3) = Total number of Stage II iterations.

result(4) = Smallest error sum of squares after Stage II training.

If training is unsuccessful, NULL is returned.

Input Keywords

Grad_tol—A scalar float defining the scaled gradient tolerance in the optimizer. Default: Grad_tol = ε1∕2, where ε is the machine precision, ε1∕3 is used in double precision.

Max_fcn—A scalar long value indicating the maximum number of function evaluations in the optimizer, per epoch. Default: Max_fcn = 400.

Max_itn—A scalar long value indicating the maximum number of iterations in the optimizer, per epoch. Default: Max_itn = 1000.

Max_step—A scalar float value indicating the maximum allowable step size in the optimizer. Default: Max_step = 1000.

No_stage_II—If present and non-zero, Stage II training is not performed. By default, in Stage I, network weights are learned using a steepest descent optimization. Stage II begins with these weights and uses a Quasi-Newton optimization to seek improved values. Default: Stage II training is performed.

Print—If present and nonzero, this option turns on printing of the intermediate results during network training. By default, intermediate results are not printed.

Rel_fcn_tol—A scalar float defining the relative function tolerance in the optimizer. By default the tolerance is: Rel_fcn_tol = max (10-10, ε2/3), max (10-20, ε2/3) in double precision, where ε is the machine precision.

Tolerance—A scalar float value indicating the absolute accuracy tolerance for the sum of squared errors in the optimizer. Default: Tolerance = 0.1.

Stage_I—A two element integer array, [n_epochs, epoch_size], where n_epochs is the number of epochs used for Stage I training and epoch_size is the number of observations used during each epoch. If epoch training is not needed, set epoch_size = n_patterns and n_epochs = 1. By default, n_epochs = 15, epoch_size = n_patterns.

Init_weights_method—Specifies the algorithm to use for initializing weights. Init_weights_method contains the weight initialization method to be used. Valid values for Init_weights_method are listed in Table 14-19: Init_weights_method Values.

Init_weights_method Values
Value	Enumeration	Description
0	IMSLS_NN_NETWORK	No initialization method will be performed. Weights in NN_Network structure network will be used instead.
1	IMSLS_EQUAL	Equal weights
2	IMSLS_RANDOM	Random Weights
3	IMSLS_PRINCIPAL_COMPONENTS	Principal Component Weights

See the MLFF_INITIALIZE_WEIGHTS Function for a detailed description of the initialization methods. Default: Init_weights_method = IMSLS_RANDOM.

Output Keywords

Residuals—Array of size n_patterns by n_outputs containing the residuals for each observation in the training data, where n_outputs is the number of output perceptrons in the network:

n_outputs = network.n_outputs

Gradients—Array of size n_links + n_nodes – n_inputs containing the gradients for each weight found at the optimum training stage, where:

n_links = network.n_links

n_nodes = network.n_nodes

n_inputs = network.n_inputs

Weights—This keyword has been deprecated starting with version 10.0 of PV-WAVE.

Forecasts—Array of size n_patterns by n_outputs, where n_outputs is the number of output perceptrons in the network:

n_outputs = network.layers(network.n_layers-1).n_nodes

The values of the ith row are the forecasts for the outputs for the ith training pattern.

Discussion

MLFF_NETWORK_TRAINER trains a multilayered feedforward neural network returning the forecasts for the training data, their residuals, the optimum weights and the gradients associated with those weights. Linkages among perceptrons allow for skipped layers, including linkages between inputs and perceptrons. The linkages and activation function for each perceptron, including output perceptrons, can be individually configured. For more details, see the Link_all, Link_layer, and Link_node keywords in MLFF_NETWORK Function.

Training Data

Neural network training patterns consist of the following three types of data:

1. categorical input attributes

2. continuous input attributes

3. continuous output classes

The first data type contains the encoding of any nominal input attributes. If binary encoding is used, this encoding consists of creating columns of zeros and ones for each class value associated with every nominal attribute. If only one attribute is used for input, then the number of columns is equal to the number of classes for that attribute. If more columns appear in the data, then each nominal attribute is associated with several columns, one for each of its classes.

Each column consists of zeros, if that classification is not associated with this case, otherwise, one if that classification is associated. Consider an example with one nominal variable and two classes: male and female (male, male, female, male, female). With binary encoding, the following matrix is sent to the training engine to represent this data:

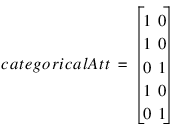
Continuous input and output data is passed to the training engine using two double precision arrays: continuous and outputs. The number of rows in each of these matrices is n_observations. The number of columns in continuous and outputs, corresponds to the number of input and output variables, respectively.

Network Configuration

The network configuration consists of the following:

the number of inputs and outputs

the number of hidden layers

a description of the number of perceptrons in each layer

and a description of the linkages among the perceptrons

This description is passed into MLFF_NETWORK_TRAINER using the structure NN_Network. See the MLFF_NETWORK Function.

Training Efficiency

The training efficiency determines the time it takes to train the network. This is controlled by several factors. One of the most important factors is the initial weights used by the optimization algorithm. These are taken from the initial values provided in the structure NN_Network, network.links(i).weight. Equally important are the scaling and filtering applied to the training data.

In most cases, all variables, particularly output variables, should be scaled to fall within a narrow range, such as [0, 1]. If variables are unscaled and have widely varied ranges, then numerical overflow conditions can terminate network training before an optimum solution is calculated.

Output

Output from MLFF_NETWORK_TRAINER consists of scaled values for the network outputs, a corresponding forecast array for these outputs, a weights array for the trained network, and the training statistics. The NN_Network structure is updated with the weights and bias values and can be used as input to the MLFF_NETWORK_FORECAST Function. For more details about the weights and bias values, see Table 14-17: Structure Members and Their Descriptions.

Example

This example trains a two-layer network using 100 training patterns from one nominal and one continuous input attribute. The nominal attribute has three classifications which are encoded using binary encoding. This results in three binary network input columns. The continuous input attribute is scaled to fall in the interval [0,1].

The network training targets were generated using the relationship:

Y = 10*X1 + 20*X2 + 30*X3 + 2.0*X4

where X1, X2, X3 are the three binary columns, corresponding to the categories 1-3 of the nominal attribute, and X4 is the scaled continuous attribute.

The structure of the network consists of four input nodes and two layers, with three perceptrons in the hidden layer and one in the output layer. Figure 14-9: A 2-layer, Feedforward Network with 4 Inputs and 1 Output illustrates this structure:

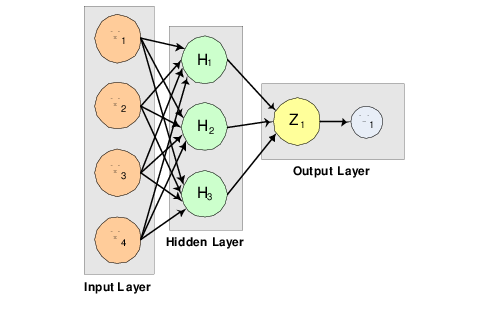Figure 14-9: A 2-layer, Feedforward Network with 4 Inputs and 1 Output

There are a total of 15 weights and 4 bias weights in this network. In the output below 19 weight values are printed. Weights 0–14 correspond to the links between the network nodes. Weights 15–18 correspond to the bias values associated with the four non-input layer nodes, X4, X5, X6, and X7. The activation functions are all linear.

Since the target output is a linear function of the input attributes, linear activation functions guarantee that the network forecasts will exactly match their targets. Of course, the same result could have been obtained using multiple regression. Printing (the Print keyword is set to 1) is turned on to show progress during the training session.

n_obs  = 100

n_cat  = 3

n_cont = 1

categorical = [ $

   1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, $

   0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, $

   0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, $

   1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, $

   0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, $

   0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, $

   0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, $

   0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, $

   1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, $

   0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, $

   1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, $

   0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, $

   0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, $

   1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, $

   0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1]

; To see the categorical 3-element vars by row, do:

; PM, TRANSPOSE(REFORM(categorical, 3,100))

continuous = [ $

   4.007054658, 7.10028447,  4.740350984, 5.714553211, $

   6.205437459, 2.598930065, 8.65089967,  5.705787357, $

   2.513348184, 2.723795955, 4.1829356,   1.93280416, $

   0.332941608, 6.745567628, 5.593588463, 7.273544478, $

   3.162117939, 4.205381208, 0.16414745,  2.883418275, $

   0.629342241, 1.082223406, 8.180324708, 8.004894314, $

   7.856215418, 7.797143157, 8.350033996, 3.778254431, $

   6.964837082, 6.13938006,  0.48610387,  5.686627923, $

   8.146173848, 5.879852653, 4.587492779, 0.714028533, $

   7.56324211,  8.406012623, 4.225261454, 6.369220241, $

   4.432772218, 9.52166984,  7.935791508, 4.557155333, $

   7.976015058, 4.913538616, 1.473658514, 2.592338905, $

   1.386872932, 7.046051685, 1.432128376, 1.153580985, $

   5.6561491,   3.31163251,  4.648324851, 5.042514515, $

   0.657054195, 7.958308093, 7.557870384, 7.901990083, $

   5.2363088,   6.95582150,  8.362167045, 4.875903563, $

   1.729229471, 4.380370223, 8.527875685, 2.489198107, $

   3.711472959, 4.17692681,  5.844828801, 4.825754155, $

   5.642267843, 5.339937786, 4.440813223, 1.615143829, $

   7.542969339, 8.100542684, 0.98625265,  4.744819569, $

   8.926039258, 8.813441887, 7.749383991, 6.551841576, $

   8.637046998, 4.560281415, 1.386055087, 0.778869034, $

   3.883379045, 2.364501589, 9.648737525, 1.21754765, $

   3.908879368, 4.253313879, 9.31189696,  3.811953836, $

   5.78471629,  3.414486452, 9.345413015, 1.024053777]

continuous = continuous/10.0

output = FLTARR(n_obs, /Nozero)

FOR i=0L, n_obs-1 DO output(i) = (10 * categorical(i*3)) $

   + (20 * categorical(i*3+1)) $

   + (30 * categorical(i*3+2)) $

   + (20 * continuous(i))

; Reform the categorical array to be 2D (three columns

; corresponding to the three categorical variables, 100

; observations each.

categorical = TRANSPOSE(REFORM(categorical, 3,100))

ff_net = MLFF_NETWORK_INIT(4, 1)

ff_net = MLFF_NETWORK(ff_net, Create_hidden_layer=3)

ff_net = MLFF_NETWORK(ff_net, /Link_all)

ff_net = MLFF_NETWORK(ff_net, Activation_fcn_layer_id=1, $

   Activation_fcn_values=[1,1,1])

RANDOMOPT, Set=12345

stats = MLFF_NETWORK_TRAINER(ff_net, $

   categorical, $

   continuous, $

   output, $

   /Print, $

   Rel_fcn_tol=1.0e-20, $

   Grad_tol=1.0e-20, $

   Max_step=5.0, $

   Max_fcn=1000, $

   Tolerance=1.0e-5, $

   Stage_I=[10,100], $

   Forecasts=forecasts, $

   Residuals=residuals)

PRINT, 'Error sum of squares at the optimum: ', stats(0)

PRINT, 'Total number of Stage I iterations:  ', stats(1)

PRINT, 'Smallest error sum of squares after Stage I training: ', $

   stats(2)

PRINT, 'Total number of Stage II iterations: ', stats(3)

PRINT, 'Smallest error sum of squares after Stage II ' + $

   'training: ', stats(4)

PRINT

PM, [[output(90:99)], [forecasts(90:99)], [residuals(90:99)]], $

   Title='Model Fit for Last Ten Observations:'

Output

 TRAINING PARAMETERS:

  Stage II Opt.   = 1

  n_epochs        = 10

  epoch_size      = 100

  max_itn         = 1000

  max_fcn         = 1000

  max_step        = 5.000000

  rfcn_tol        = 1e-020

  grad_tol        = 1e-020

  tolerance       = 0.000010

STAGE I TRAINING STARTING

Stage I: Epoch 1 - Epoch Error SS = 4349.96 (Iterations=7)

Stage I: Epoch 2 - Epoch Error SS = 3406.89 (Iterations=7)

Stage I: Epoch 3 - Epoch Error SS = 4748.62 (Iterations=7)

Stage I: Epoch 4 - Epoch Error SS = 1825.62 (Iterations=7)

Stage I: Epoch 5 - Epoch Error SS = 3353.35 (Iterations=7)

Stage I: Epoch 6 - Epoch Error SS = 3771.22 (Iterations=7)

Stage I: Epoch 7 - Epoch Error SS = 2769.11 (Iterations=7)

Stage I: Epoch 8 - Epoch Error SS = 3781.3 (Iterations=9)

Stage I: Epoch 9 - Epoch Error SS = 2404.1 (Iterations=7)

Stage I: Epoch 10 - Epoch Error SS = 4350.14 (Iterations=7)

STAGE I FINAL ERROR SS = 1825.617676

OPTIMUM WEIGHTS AFTER STAGE I TRAINING:

weight[0] = -2.31313 weight[1] = 0.389252   weight[2] = 1.89219

weight[3] = 1.76989 weight[4] = -0.975819   weight[5] = 0.91344

weight[6] = 2.38119 weight[7] = 1.42829    weight[8] = -2.60983

weight[9] = 1.09477 weight[10] = 3.04915   weight[11] = 2.49006

weight[12] = 7.95465 weight[13] = 10.7354 weight[14] = 10.2354

weight[15] = -0.614357 weight[16] = 1.22405

weight[17] = 1.72196 weight[18] = 4.6308

STAGE II TRAINING USING QUASI-NEWTON

STAGE II FINAL ERROR SS = 0.319787

OPTIMUM WEIGHTS AFTER STAGE II TRAINING:

weight[0] = -6.81913 weight[1] = -7.35462 weight[2] = -3.6998

weight[3] = 5.64984 weight[4] = -0.740951 weight[5] = 1.21874

weight[6] = -0.726229 weight[7] = 4.05967 weight[8] = -2.42175

weight[9] = -0.580469 weight[10] = 4.85256 weight[11] = 3.45859

weight[12] = 10.4209 weight[13] = 16.9226 weight[14] = 20.8385

weight[15] = -0.944827 weight[16] = -0.143303

weight[17] = -1.44022 weight[18] = 4.91185

GRADIENT AT THE OPTIMUM WEIGHTS

g[0] =   0.031620        weight[0] =    -6.819134

g[1] =  -0.245708        weight[1] =    -7.354622

g[2] =  -0.551255        weight[2] =    -3.699798

g[3] =  -0.550290        weight[3] =     5.649842

g[4] =   1.109601        weight[4] =    -0.740951

g[5] =   0.120410        weight[5] =     1.218741

g[6] =  -2.830182        weight[6] =    -0.726229

g[7] =  -0.902171        weight[7] =     4.059670

g[8] =   0.197736        weight[8] =    -2.421750

g[9] =   1.453753        weight[9] =    -0.580469

g[10] = -0.178615        weight[10] =    4.852565

g[11] =  0.208161        weight[11] =    3.458595

g[12] = -0.166397        weight[12] =   10.420921

g[13] = -0.396238        weight[13] =   16.922632

g[14] = -0.924226        weight[14] =   20.838531

g[15] = -0.765342        weight[15] =   -0.944827

g[16] = -1.600171        weight[16] =   -0.143303

g[17] =  1.472873        weight[17] =   -1.440215

g[18] = -0.417480        weight[18] =    4.911847

Training Completed

Error sum of squares at the optimum:       0.319787

Total number of Stage I iterations:         7.00000

Smallest error sum of squares after Stage I training:   1825.62

Total number of Stage II iterations:        1015.00

Smallest error sum of squares after Stage II training: 0.319787

Model Fit for Last Ten Observations:

       49.2975       49.0868     -0.210632

       32.4351       32.3968    -0.0383034

       37.8178       37.7850    -0.0328064

       38.5066       38.4759    -0.0307388

       48.6238       48.5395    -0.0843124

       37.6239       37.5900    -0.0339203

       41.5694       41.5405    -0.0289001

       36.8290       36.7881    -0.0409050

       48.6908       48.5958    -0.0950241

       32.0481       32.0286    -0.0194893