GAMMAI Function
Evaluates the incomplete gamma function γ(a, x).
Usage
result = GAMMAI(a, x)
Input Parameters
a—Integrand exponent parameter. It must be positive.
x—Upper limit of integration. It must be nonnegative.
Returned Value
result—The value of the incomplete gamma function γ(a, x).
Input Keywords
Double—If present and nonzero, double precision is used.
Discussion
The incomplete gamma function, γ(a, x), is defined as follows:
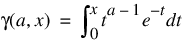
The incomplete gamma function is defined only for a > 0. Although γ(a, x) is well-defined for x > –infinity, this algorithm does not calculate γ(a, x) for negative x. For large a and sufficiently large x, γ(a, x) may overflow. Gamma function γ(a, x) is bounded by Γ(a), and users may find this bound a useful guide in determining legal values for a.
Example
Plot the incomplete gamma function over [0.1, 1.1] × [0, 4]. The results are shown in Figure 10-4: Imcomplete Gamma Function Plot.
x = 4. * FINDGEN(25)/24
a = 1e-1 + FINDGEN(25)/24
b = FLTARR(25, 25)
FOR i=0L, 24 DO b(i, *) = GAMMAI(a(i), x)
!P.Charsize = 2.5
SURFACE, b, a, x, XTitle = 'a', YTitle = 'X'
 |
Fatal Errors
MATH_NO_CONV_200_TS_TERMS—Function did not converge in 200 terms of Taylor series.
MATH_NO_CONV_200_CF_TERMS—Function did not converge in 200 terms of the continued fraction.