ERFC Function
Evaluates the real complementary error function erfc(x). Using a keyword, the inverse complementary error function erfc–1(x) can be evaluated.
Usage
result = ERFC(x)
Input Parameters
x—Expression for which the complementary error function is to be evaluated.
Returned Value
result—The value of the complementary error function erfc(x).
Input Keywords
Double—If present and nonzero, double precision is used.
Inverse—Evaluates the inverse complementary error function erfc–1(x). The parameter must be in the range 0 < x < 2.
Discussion
The complementary error function erfc(x) is defined as:
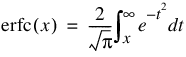
where parameter x must not be so large that the result underflows. Approximately, x should be less than:
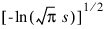
where s is the smallest representable floating-point number.
The inverse complementary error function y = erfc–1(x) is such that x = erfc(y).
Example 1
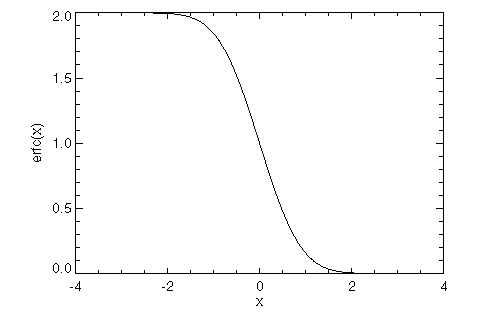
Plot the complementary error function over [–3, 3]. The results are shown in Figure 10-1: Plot of erf(x).
x = FINDGEN(100)/99
PLOT, 6 * x - 3, ERFC(6 * x - 3), XTitle = 'x', YTitle = 'erfc(x)'
 |
Example 2
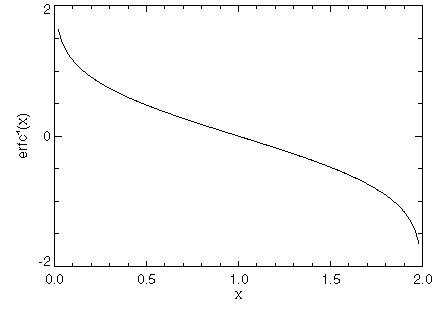
Plot the inverse of the complementary error function over (0, 2). The results are shown in Figure 10-2: Plot of erfc–1(x).
x = FINDGEN(100)/99
PLOT, 2 * x(1:98), ERFC(2 * x(1:98), /Inverse), XTitle = 'x', $
YTitle = 'erfc!E-1!N(x)'
 |
Alert Errors
MATH_LARGE_ARG_UNDERFLOW—Parameter x must not be so large that the result underflows. Very approximately, x should be less than:
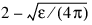
where ε is the machine precision.
Warning Errors
MATH_LARGE_ARG_WARN—Parameter |x| should be less than
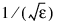
where ε is the machine precision, to prevent the answer from being less accurate than half precision.
Fatal Errors
MATH_ERF_ALGORITHM—Algorithm failed to converge.
MATH_SMALL_ARG_OVERFLOW—Computation of:
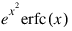
must not overflow.
MATH_REAL_OUT_OF_RANGE—Function is defined only for 0 < x < 2.





