CLUSTER_NUMBER Function
Computes cluster membership for a hierarchical cluster tree.
Usage
result = CLUSTER_NUMBER(clson, crson, k)
Input Parameters
clson—Vector of length npt – 1 containing the left son cluster numbers, where npt is the number of data points to be clustered. Cluster npt + i is formed by merging clusters clson(i – 1) and crson(i – 1).
crson—Vector of length npt – 1 containing the right son cluster numbers. Cluster npt + i is formed by merging clusters clson(i – 1) and crson(i – 1).
k—Desired number of clusters.
Returned Value
result—Long vector of length npt containing the cluster membership of each observation.
Output Keywords
Obs_per_cluster—Array of length K containing the number of observations in each cluster.
Discussion
Given a fixed number of clusters (K) and the cluster tree (vectors crson and clson) produced by the hierarchical clustering algorithm (see CLUSTER_HIERARCHICAL Procedure) CLUSTER_NUMBER determines the cluster membership of each observation. It first determines the root nodes for the K distinct subtrees forming the K clusters and then traverses each subtree to determine the cluster membership of each observation. CLUSTER_NUMBER also returns the number of observations found in each cluster.
Example 1
In the following example, cluster membership for K = 2 clusters is found for the displayed cluster tree. The output vector iclus contains the cluster numbers for each observation.
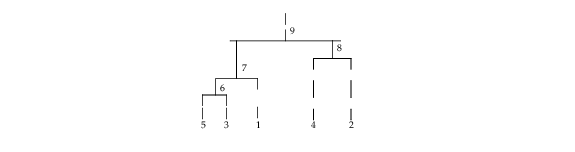
; Set up the input data
k = 2
iclson = [5, 6, 4, 7]
icrson = [3, 1, 2, 8]
; Call the CLUSTER_NUMBER routine
iclus = CLUSTER_NUMBER(iclson, icrson, k, Obs_per_cluster=nclus)
PRINT,""
PRINT," OUTPUT"
PRINT," ----------"
PRINT,""
PRINT," iclus"
PRINT,iclus, Format="(5I5)"
Output
OUTPUT
----------
iclus
1 2 1 2 1
Example 2
This example illustrates the typical usage of CLUSTER_NUMBER. The Fisher iris data is clustered. First the distance between the irises are computed using DISSIMILARITIES. The resulting distance matrix is then clustered using CLUSTER_HIERARCHICAL. The cluster membership for 5 clusters is then obtained via CLUSTER_NUMBER using the output from CLUSTER_HIERARCHICAL. The need for 5 clusters can be obtained either by theoretical means or by examining a cluster tree. The cluster membership for each of the iris observations is printed.
data = STATDATA(3)
k = 5
dist = DISSIMILARITIES(data,Index=[1,2,3,4])
RANDOMOPT,Set=4
FOR i=0L, 149 DO BEGIN & $
FOR j=i+1, 149 DO BEGIN & $
r = RANDOM(1, /Uniform) & $
dist(i,j) = MAX([0.0, dist(i,j) + .001 * r]) & $
dist(j,i) = dist(i,j) & $
ENDFOR & $
dist(i,i) = 0. & $
ENDFOR
CLUSTER_HIERARCHICAL, dist, Clevel=clevel, Clson=clson, $
Crson=crson
iclus = CLUSTER_NUMBER(clson, crson, k, Obs_per_cluster=nclus)
PRINT,""
PRINT," OUTPUT"
PRINT," ----------"
PRINT,""
PRINT," ICLUS"
PRINT,iclus,Format='(5I3)'
PRINT,""
PRINT," NCLUS"
PRINT,nclus,Format='(5I4)'
Output
OUTPUT
----------
ICLUS
5 5 5 5 5
5 5 5 5 5
5 5 5 5 5
5 5 5 5 5
5 5 5 5 5
5 5 5 5 5
5 5 5 5 5
5 5 5 5 5
5 5 5 5 5
5 5 5 5 5
2 2 2 2 2
2 2 1 2 2
1 2 2 2 2
2 2 2 2 2
2 2 2 2 2
2 2 2 2 2
2 2 2 2 2
2 2 2 2 2
2 2 2 1 2
2 2 2 1 2
2 2 2 2 2
2 3 2 2 2
2 2 2 2 2
2 2 4 2 2
2 2 2 2 2
2 2 2 2 2
2 4 2 2 2
2 2 2 2 2
2 2 2 2 2
2 2 2 2 2
NCLUS
4 93 1 2 50