DISSIMILARITIES Function
Computes a matrix of dissimilarities (or similarities) between the rows (or columns) of a matrix.
Usage
result = dissimilarities (x)
Input Parameters
x—Array of size nrow by ncol containing the matrix.
Returned Value
result—Float or double array of size m by m containing the computed dissimilarities or similarities, where m = nrow (the default) or m = ncol, if the Columns keyword is specified.
Input Keywords
Double—If present and nonzero, double precision is used.
Columns—Determines whether distances are computed between rows or columns of x. Default: Distances are computed between rows.
Index—An input array containing the indices of the rows (or columns if the Columns keyword is set) to be used in computing the distance measure. Default: All rows(columns) are used.
Method—Method for computing the dissimilarities or similarities. See the Discussion section for more information. Default: Method = 0.
Scale—Scaling option. Scale is not used for methods 3 through 8. Default: Scale = 0.
Discussion
DISSIMILARITIES computes an upper triangular matrix (excluding the diagonal) of dissimilarities (or similarities) between the rows or columns of a matrix. Nine different distance measures can be computed. For the first three measures, three different scaling options can be employed. Output from DISSIMILARITIES is generally used as input to clustering or multidimensional scaling functions.
The following discussion assumes that the distance measure is being computed between the columns of the matrix, i.e., that the Columns keyword is set. If distances between the rows of the matrix are desired, leave the Columns keyword set to the default.
For Method = 0 to 2, each row of x is first scaled according to the value of Scale. The scaling parameters are obtained from the values in the row scaled as either the standard deviation of the row or the row range; the standard deviation is computed from the unbiased estimate of the variance. If Scale is 0, no scaling is performed, and the parameters in the following discussion are all 1.0. Once the scaling value (if any) has been computed, the distance between column i and column j is computed via the difference vector zk = (xk - yk)/sk, i = 1, ..., Ndstm, where:
For given zi, the metrics 0 to 2 are defined as:
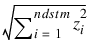 Euclidean distance
Euclidean distance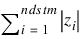 L1 norm
L1 norm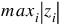 L∞ norm
L∞ normDistance measures corresponding to Method = 3 through 8 do not allow for scaling. These measures are defined via the column vectors X = (xi), Y = (yi), and Z = (xi - yi) as follows:
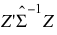 = Mahalanobis distance, where
= Mahalanobis distance, where 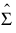 is the usual unbiased sample estimate of the covariance matrix of the rows.
is the usual unbiased sample estimate of the covariance matrix of the rows.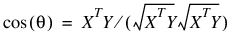 = the dot product of X and Y divided by the length of X times the length of Y.
= the dot product of X and Y divided by the length of X times the length of Y.For the Mahalanobis distance, any variable used in computing the distance measure that is (numerically) linearly dependent upon the previous variables in the Index vector is omitted from the distance measure.
Example
The following example illustrates the use of DISSIMILARITIES for computing the Euclidean distance between the rows of a matrix.
ncol = 2
nrow = 4
; Create an NROW x NCOL data set.
x = [[1., 1., 1., 1.], [1., 0., -1., 2.]]
; Call the routine using the default, Row orientation,
; no scaling and the
; 'Sum of the Absolute Differences' method
dist = DISSIMILARITIES(x, ind=[0,1], scale=0, method=1)
; Show the output
PRINT,""
PRINT," OUTPUT"
PRINT," -------------------"
PRINT,""
PRINT," dist"
PM, dist, Format="(4I)"
Output
OUTPUT
-------------------
dist
0 1 2 1
0 0 1 2
0 0 0 3
0 0 0 0





